题目内容
若等差数列{an}各项均为正，且a3a5+a3a8+a5a10+a8a10=64，则S12= ．
考点：等差数列的性质,等差数列的前n项和
专题：等差数列与等比数列
分析：把已知等式因式分解求得a5+a8=8，然后把S12化为含有a5+a8的代数式得答案．
解答：
解：a3a5+a3a8+a5a10+a8a10=（a3a5+a3a8）+（a5a10+a8a10）
=a3（a5+a8）+a10（a5+a8）=（a5+a8）（a3+a10）=64，
∵{an}为等差数列，故a3+a10=a5+a8，
故(a5+a8)2=64，又∵an＞0，
故a5+a8=8，
∴S12=（a1+a12）+（a2+a11）+…+（a6+a7）=6（a5+a8）=48．
故答案为：48．
=a3（a5+a8）+a10（a5+a8）=（a5+a8）（a3+a10）=64，
∵{an}为等差数列，故a3+a10=a5+a8，
故(a5+a8)2=64，又∵an＞0，
故a5+a8=8，
∴S12=（a1+a12）+（a2+a11）+…+（a6+a7）=6（a5+a8）=48．
故答案为：48．
点评：本题考查了等差数列的性质，考查了学生的灵活变形能力，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若执行如图的程序框图，输出S的值为4，则判断框中应填入的条件是（ ）
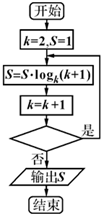
| A、k＜14？ |
| B、k＜15？ |
| C、k＜16？ |
| D、k＜17？ |
已知实数x、y满足
，则z=（x-1）2+（y-2）2的最小值为（ ）
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin（2x+ϕ）的图象沿x轴向左平移
个单位后，得到一个偶函数的图象，则ϕ的一个可能取值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
| C、0 | ||
D、-
|
设两个向量
=（n+2，n-cos2x），
=（m，
+sinx），其中m，n为实数，若存在实数x使得
=2
，则m的取值范围为（ ）
| a |
| b |
| m |
| 2 |
| a |
| b |
| A、[1，4] |
| B、[0，4] |
| C、[0，2] |
| D、[-6，-2] |
已知条件p：y=lg（x2+2x-3）的定义域，条件q：5x-6＞x2，则￢p是￢q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合A={{x|y=
}，集合B={x||x-2|＜2}，则A∩B等于（ ）
| 2+x-x2 |
| A、（0，2] | B、[0，2] |
| C、[-1，2） | D、∅ |
函数y=x2-4ax+1在区间[-2，4]上单调递增函数，则实数a的取值范围是（ ）
| A、（-∞，2] |
| B、（-∞，-1] |
| C、[2，+∞） |
| D、[-1，+∞） |