题目内容
解方程
+
=1．
| 15 |
| 27-λ |
| 16 |
| 36-λ |
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：直接化简方程为二次方程，然后求解即可．
解答：
解：
+
=1．
可得15（36-λ）+16（27-λ）=（36-λ）（27-λ），
即：λ2-32λ=0，
解得λ=0或λ=32．
| 15 |
| 27-λ |
| 16 |
| 36-λ |
可得15（36-λ）+16（27-λ）=（36-λ）（27-λ），
即：λ2-32λ=0，
解得λ=0或λ=32．
点评：本题考查函数的零点与方程根的关系，基本知识的考查．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
设a=log23.9，b=log20.7，c=2，则（ ）
| A、b＜a＜c |
| B、a＜b＜c |
| C、c＜a＜b |
| D、c＜b＜a |
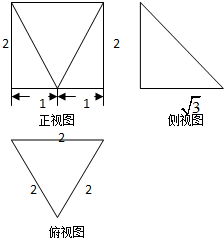一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）| A、9π | ||
B、
| ||
| C、8π | ||
| D、7π |
已知在△ABC中，D是AB边上的一点，
=λ（
+
），|
|=2，|
|=1，若
=
，
=
，则用
，
表示
为（ ）
| CD |
| ||
|
|
| ||
|
|
| CA |
| CB |
| CA |
| b |
| CB |
| a |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|