题目内容
3．函数y=loga（x+1）+x2-2（0＜a＜1）的零点的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 无法确定 |
分析 令loga（x+1）+x2-2=0，方程解的个数即为所求函数零点的个数．即考查图象y=loga（x+1）与y=-x2+2的交点个数即可．
解答 
解：由y=loga（x+1）+x2-2=0，
得loga（x+1）=-x2+2，
作出函数y=loga（x+1），0＜a＜1和y=-x2+2的图象，由图象知，
两个函数的图象有2个交点，
即函数y=loga（x+1）+x2-2（0＜a＜1）的零点的个数为2个，
故选：C
点评 本题主要考查函数零点个数的判断，根据函数与方程之间的关系转化为两个函数交点个数问题是解决本题的关键．
练习册系列答案
优等生题库系列答案
相关题目
18．在等腰直角△ABC中，过顶点C的直线l与斜边AB相交的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
15．
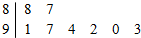某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）
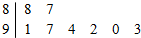某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）| A． | 91 5.5 | B． | 91 5 | C． | 92 5.5 | D． | 92 5 |
12．使得函数f（x）=log2x+x-5有零点的一个区间是（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
13．已知扇形的中心角为$\frac{π}{3}$，半径为2，则其面积为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{4π}{3}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |