题目内容
8.已知各项为正的等比数列{an}的前n项和为Sn,S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(-1,-1)(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{log}_{2}{a}_{n+2}•{log}_{2}{a}_{n}}$,数列{bn}的前n项和为Tn,证明:对于任意n∈N*,都有Tn$<\frac{3}{4}$.
分析 (1)利用等比数列前n项和公式及直线的方向向量性质列出方程组,由此能求出首项和公比,从而能求出数列{an}的通项公式.
(2)由bn=$\frac{1}{{log}_{2}{a}_{n+2}•{log}_{2}{a}_{n}}$=$\frac{1}{4}$($\frac{1}{lo{g}_{2}{a}_{n}}$-$\frac{1}{lo{g}_{2}{a}_{n+2}}$),利用裂项法能证明对于任意n∈N*,都有Tn$<\frac{3}{4}$.
解答 解:(1)∵各项为正的等比数列{an}的前n项和为Sn,S4=30,
过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(-1,-1),
∴$\left\{\begin{array}{l}{\frac{{a}_{1}(1-{q}^{4})}{1-q}=30}\\{\frac{lo{g}_{2}{a}_{n+1}-lo{g}_{2}{a}_{n}}{n+2-n}=\frac{-1}{-1}}\end{array}\right.$,
解得${a}_{1}=\frac{6}{17}$,q=4,
∴an=$\frac{6}{17}×{4}^{n-1}$.
(2)∵bn=$\frac{1}{{log}_{2}{a}_{n+2}•{log}_{2}{a}_{n}}$=$\frac{1}{(lo{g}_{2}\frac{6}{17}+2n+2)(lo{g}_{2}\frac{6}{17}+2n-2)}$=$\frac{1}{4}$($\frac{1}{lo{g}_{2}{a}_{n}}$-$\frac{1}{lo{g}_{2}{a}_{n+2}}$),
∴数列{bn}的前n项和:
Tn=$\frac{1}{4}$($\frac{1}{lo{g}_{2}{a}_{1}}-\frac{1}{lo{g}_{2}{a}_{3}}$+$\frac{1}{lo{g}_{2}{a}_{2}}-\frac{1}{lo{g}_{2}{a}_{4}}$+$\frac{1}{lo{g}_{2}{a}_{3}}-\frac{1}{lo{g}_{2}{a}_{5}}$+…+$\frac{1}{lo{g}_{2}{a}_{n-1}}-\frac{1}{lo{g}_{2}{a}_{n+1}}$+$\frac{1}{lo{g}_{2}{a}_{n}}-\frac{1}{lo{g}_{2}{a}_{n+2}}$)
=$\frac{1}{4}$($\frac{1}{lo{g}_{2}{a}_{1}}+\frac{1}{lo{g}_{2}{a}_{2}}$-$\frac{1}{lo{g}_{2}{a}_{n+1}}-\frac{1}{lo{g}_{2}{a}_{n+2}}$)
=$\frac{1}{4}$($\frac{1}{lo{g}_{2}\frac{6}{17}}$+$\frac{1}{lo{g}_{2}\frac{6}{17}+2}$-$\frac{1}{lo{g}_{2}\frac{6}{17}+2n}$-$\frac{1}{lo{g}_{2}\frac{6}{17}+2n+2}$)
<$\frac{3}{4}$.
∴对于任意n∈N*,都有Tn$<\frac{3}{4}$.
点评 本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

 高中必刷题系列答案
高中必刷题系列答案(1)根据所给样本数据完成下面2×2列联表;
(2)请问能否有90%把握认为药物有效?
| 不得禽流感 | 得禽流感 | 总 计 | |
| 服 药 | 40 | 20 | 60 |
| 不服药 | 20 | 20 | 40 |
| 总 计 | 60 | 40 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.001 |
| k | 2.072 | 3.841 | 6.635 | 10.828 |
| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
| A. | 0 | B. | 1 | C. | 2 | D. | 无法确定 |
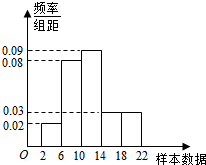 样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )| A. | 32,0.4 | B. | 8,0.1 | C. | 32,0.1 | D. | 8,0.4 |
| A. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | B. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | ||
| C. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ | D. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ |