题目内容
15．
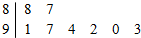某市8所中学生参加比赛的得分用茎叶图表示（如图）其中茎为十位数，叶为个位数，则这组数据的平均数和方差分别是（ ）| A． | 91 5.5 | B． | 91 5 | C． | 92 5.5 | D． | 92 5 |
分析 根据茎叶图中的数据，计算这组数据的平均数与方差即可．
解答 解：把茎叶图中的数据按大小顺序排列，如下；
87、88、90、91、92、93、94、97；
∴平均数是$\frac{1}{8}$（87+88+90+91+92+93+94+97）=91.5，
S2=$\frac{1}{8}$[（87-91.5）2+（88-91，5）2+（90-91.5）2+…+（97-91.5）2]=5，
故选：A．
点评 本题考查了利用茎叶图中的数据求方差与平均数的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
6．已知f（x）=ex+2xf′（1），则f′（0）等于（ ）
| A． | 1+2e | B． | 1-2e | C． | -2e | D． | 2e |
3．函数y=loga（x+1）+x2-2（0＜a＜1）的零点的个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 无法确定 |
10．
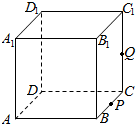如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的中点，则四面体A1PQD的正视图、侧视图和俯视图的面积之和为（ ）
如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的中点，则四面体A1PQD的正视图、侧视图和俯视图的面积之和为（ ）| A． | $\frac{5}{4}$ | B． | 2 | C． | $\frac{9}{4}$ | D． | $\frac{5}{2}$ |
20．
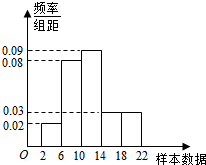样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）
样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）| A． | 32，0.4 | B． | 8，0.1 | C． | 32，0.1 | D． | 8，0.4 |
7．有5名学生的数学和化学成绩如表所示：
（1）如果y与x具有相关关系，求线性回归方程；
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| 学生学科 | A | B | C | D | E |
| 数学成绩（x） | 88 | 76 | 73 | 66 | 63 |
| 化学成绩（y） | 78 | 65 | 71 | 64 | 61 |
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．