题目内容
12．使得函数f（x）=log2x+x-5有零点的一个区间是（ ）| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
分析 由题意知函数f（x）=log2x+x-5在（0，+∞）上连续，再由函数的零点的判定定理求解．
解答 解：函数f（x）=log2x+x-5在（0，+∞）上连续，
f（3）=log23+3-5＜0；
f（4）=2+4-5＞0；
故函数f（x）=log2x+x-5的零点所在的区间是（3，4）；
故选C．
点评 本题考查了函数的零点的判定定理的应用，属于基础题．
练习册系列答案
相关题目
3．函数y=loga（x+1）+x2-2（0＜a＜1）的零点的个数为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 无法确定 |
20．
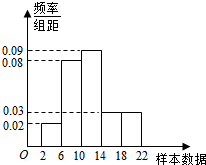样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）
样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）| A． | 32，0.4 | B． | 8，0.1 | C． | 32，0.1 | D． | 8，0.4 |
7．有5名学生的数学和化学成绩如表所示：
（1）如果y与x具有相关关系，求线性回归方程；
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| 学生学科 | A | B | C | D | E |
| 数学成绩（x） | 88 | 76 | 73 | 66 | 63 |
| 化学成绩（y） | 78 | 65 | 71 | 64 | 61 |
（2）预测如果某学生数学成绩为79分，他的化学成绩为多少？
参考公式：：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．