题目内容
若函数f(x)是R上的奇函数,且f(x)在[0,+∞)上单调递减,则集合A={x|f(log2x-1)<0}= .
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由函数f(x)是R上的奇函数,且f(x)在[0,+∞)上单调递减,可得f(x)在R上单调递减,从而f(log2x-1)<0=f(0)可化为log2x-1>0,解出即可.
解答:
解:∵函数f(x)是R上的奇函数,且f(x)在[0,+∞)上单调递减,
故f(x)在R上单调递减,
∴f(log2x-1)<0=f(0),
∴log2x-1>0,解得x>2,
故答案为:(2,+∞).
故f(x)在R上单调递减,
∴f(log2x-1)<0=f(0),
∴log2x-1>0,解得x>2,
故答案为:(2,+∞).
点评:本题考查函数的奇偶性、单调性及其应用,考查对不等式的解法,属基础题,利用性质化抽象不等式为具体不等式是解题关键.

练习册系列答案
相关题目
已知双曲线的渐近线方程为x±2y=0,则该双曲线的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
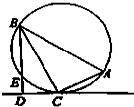 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为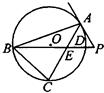 如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于
如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于