题目内容
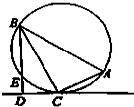 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为考点:与圆有关的比例线段
专题:选作题,立体几何
分析:设AB=2r,利用直角△ABC的边角关系即可得出BC,利用弦切角定理可得∠BCD=∠A=60°.利用直角△BCD的边角关系即可得出CD,BD.再利用切割线定理可得CD2=DE•DB,即可求出△ABC的外接圆的半径.
解答:
解:设AB=2r,则
在△ABC中,∠C=90°,∠A=60°,AB=2r,
∴BC=AB•sin60°=
r.
∵CD是此圆的切线,∴∠BCD=∠A=60°.
在Rt△BCD中,CD=BC•cos60°=
r,BD=BC•sin60°=
r.
由切割线定理可得CD2=DE•DB,
∴(
r)2=5•
r,解得r=10.
故答案为:10.
在△ABC中,∠C=90°,∠A=60°,AB=2r,
∴BC=AB•sin60°=
| 3 |
∵CD是此圆的切线,∴∠BCD=∠A=60°.
在Rt△BCD中,CD=BC•cos60°=
| ||
| 2 |
| 3 |
| 2 |
由切割线定理可得CD2=DE•DB,
∴(
| ||
| 2 |
| 3 |
| 2 |
故答案为:10.
点评:熟练掌握直角三角形的边角关系、弦切角定理、切割线定理是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
某班级要从4名男生、2名女生中选派4人参加某次社会活动,如果要求至少有1名女生.那么不同的选派方法共有( )
| A、14种 | B、28种 |
| C、32种 | D、48种 |
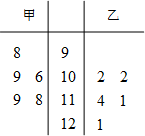 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如茎叶图所示: