题目内容
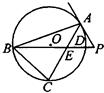 如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于
如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于考点:与圆有关的比例线段
专题:选作题,立体几何
分析:利用切割线定理结合题中所给数据,得PA=3,由弦切角定理结合有一个角为60°的等腰三角形是正三角形,得到PE=AE=3,最后由相交弦定理可得BE•DE=AE•CE,从而求出EC的长.
解答:
解:∵PA是圆O的切线,
∴PA2=PD•PB=9,可得PA=3
∵∠PAC是弦切角,夹弧ADC
∴∠PAC=∠ABC=60°,
∵△ADE中,PE=PA,
∴△APE是正三角形,可得PE=AE=PA=3
∴BE=PB-PE=6,DE=PE-PD=2
∵圆O中,弦AC、BD相交于E,
∴BE•DE=AE•CE,可得6×2=3EC,EC=4
故答案为:4.
∴PA2=PD•PB=9,可得PA=3
∵∠PAC是弦切角,夹弧ADC
∴∠PAC=∠ABC=60°,
∵△ADE中,PE=PA,
∴△APE是正三角形,可得PE=AE=PA=3
∴BE=PB-PE=6,DE=PE-PD=2
∵圆O中,弦AC、BD相交于E,
∴BE•DE=AE•CE,可得6×2=3EC,EC=4
故答案为:4.
点评:本题在圆中给出切线,并且以切线长为一边作正三角形的情况下,求线段的长度.着重考查了切线的性质、正三角形的判定和相交弦定理等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“a=3”是“函数f(x)=|3x-a|在[1,+∞)上为单调递增函数的”( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为5,则|AB|等于( )
| A、12 | B、8 | C、6 | D、4 |