题目内容
2. 如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是$\frac{π}{4}$,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )
如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是$\frac{π}{4}$,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )| A. | [$\frac{π}{4}$,$\frac{π}{2}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$] | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$] |
分析 以B为原点,BC为x轴,BA为y轴,过B作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线BD与PQ所成角的取值范围.
解答 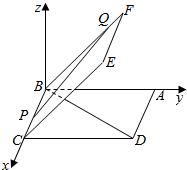 解:以B为原点,BC为x轴,BA为y轴,过B作平面ABCD的垂线为z轴,建立空间直角坐标系,
解:以B为原点,BC为x轴,BA为y轴,过B作平面ABCD的垂线为z轴,建立空间直角坐标系,
设BC=1,则B(0,0,0),D(1,1,0),C(1,0,0),
E(1,$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$),F(0,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
当D点在正方形BCEF的投影刚好落在CE上,记为G点,其坐标为G(1,$\frac{1}{2}$,$\frac{1}{2}$),
此时BG与BD所成角刚好30度,
即直线BD与PQ所成角的最小值为$\frac{π}{6}$,
取P($\frac{1}{2}$,0,0),Q(0,$\frac{1}{2},\frac{1}{2}$)时,直线BD于PQ所成角取最大值,
∵$\overrightarrow{BD}$=(1,1,0),$\overrightarrow{PQ}$=(-$\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$),
∴cos<$\overrightarrow{BD},\overrightarrow{PQ}$>=$\frac{\overrightarrow{BD}•\overrightarrow{PQ}}{|\overrightarrow{BD}|•|\overrightarrow{PQ}|}$=0,
∴直线BD于PQ所成角最大值为$\frac{π}{2}$.
∴直线BD与PQ所成角的取值范围是[$\frac{π}{6}$,$\frac{π}{2}$].
故选:B.
点评 本题考查异面直线所成角的取值范围的求法,则中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | (2,1) | B. | (1,2) | C. | (0,$\sqrt{3}$) | D. | ($\sqrt{3}$,0) |
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
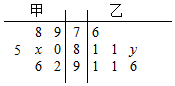 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.