题目内容
7．
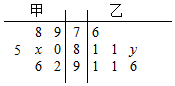高三年级从甲（文）、乙（理）两个科组各选出7名学生参加高校自主招生数学选拔考试，他们取得的成绩的茎叶图如图所示，其中甲组学生的平均分是85，乙组学生成绩的中位数是83．（1）求x和y的值；
（2）计算甲组7位学生成绩的方差S2．
分析 （1）根据甲组学生的平均分求出x的值，根据乙组学生成绩的中位数得出y的值；
（2）根据公式计算甲组成绩的平均数和方差即可．
解答 解：（1）∵甲组学生的平均分是85，
∴$\frac{1}{7}$（78+79+80+80+x+85+92+96）=85；
解得x=5；
又乙组学生成绩的中位数是83，∴y=3；
（2）甲组成绩的平均数是85，
方差是S2=$\frac{1}{7}$[（78-85）2+（79-85）2+（80-85）2+（85-85）2+（85-85）2+（92-85）2+（96-85）2]=40．
点评 本小题主要考查了利用茎叶图中的数据求平均数、中位数与方差的问题，是基础题目．
练习册系列答案
相关题目
17．定义在（1，+∞）上的函数f（x）满足：①f（2x）=cf（x）（c为正常数）； ②当2≤x≤4时，f（x）=1-（x-3）2，若f（x）图象上所有极大值对应的点均落在同一条直线上，则c=（ ）
| A． | 1或$\frac{1}{2}$ | B． | $\frac{1}{2}$或2 | C． | 1或2 | D． | 1或3 |
2．
如图，正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是$\frac{π}{4}$，PQ是正方形BDEF所在平面内的一条动直线，则直线BD与PQ所成角的取值范围是（ ）
如图，正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是$\frac{π}{4}$，PQ是正方形BDEF所在平面内的一条动直线，则直线BD与PQ所成角的取值范围是（ ）| A． | [$\frac{π}{4}$，$\frac{π}{2}$] | B． | [$\frac{π}{6}$，$\frac{π}{2}$] | C． | [$\frac{π}{6}$，$\frac{π}{3}$] | D． | [$\frac{π}{3}$，$\frac{π}{2}$] |