题目内容
18.定义在R上的奇函数f(x)满足f(2-x)=f(x),当x∈[0,1]时,f(x)=$\sqrt{x}$.又函数g(x)=cos$\frac{πx}{2}$,x∈[-3,3],则函数F(x)=f(x)-g(x)的所有零点之和等于( )| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
分析 利用奇偶性和对称性作出f(x)和g(x)的函数图象,利用周期性得出F(x)的零点间的关系,计算F(x)在(0,1)上的零点即可得出零点之和.
解答 解:∵f(2-x)=f(x),
∴f(x)的图象关于直线x=1对称,
又f(x)是奇函数,
∴f(x)=f(2-x)=-f(x-2),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)的周期为4.
作出f(x)和g(x)在[-3,3]上的函数图象如图所示: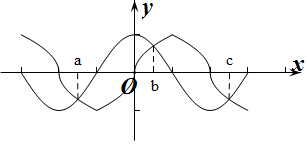
由图象可知f(x)=g(x)在[-3,3]上有3个零点,
不妨设a,b,c且a<b<c,
∵f(x)和g(x)都是周期为4的函数,
∴a=b-2,c=b+2,
∴a+b+c=3b.
∵f($\frac{1}{2}$)=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,g($\frac{1}{2}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
∴b=$\frac{1}{2}$,
∴a+b+c=3b=$\frac{3}{2}$.
故选D.
点评 本题考查了函数零点与函数图象的关系,函数周期与对称性性的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.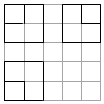 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
13.已知(x-2)6=a0+a1(x-1)+a2(x-1)2+…+a6(x-1)6,则a3=( )
| A. | 15 | B. | -15 | C. | 20 | D. | -20 |
3.已知集合A={x|x2-x-2<0},$B=\left\{{x|{{log}_4}x<\frac{1}{2}}\right\}$,则( )
| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
10.福利彩票“双色球”中红色球的号码由编号为01,02,…,33的33个个体组成,小明利用下面的随机数表选取6组数作为6个红色球的编号,选取方法是从随机数表第1行的第7列数字开始由左到右依次读取数据,则选出来的第3个红色球的编号为( )
| 49 54 43 54 15 37 17 93 39 78 87 35 20 96 43 84 17 34 91 64 |
| 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
| A. | 06 | B. | 17 | C. | 20 | D. | 24 |
7.已知$α∈(\frac{π}{3},π)$,且$sin(α+\frac{π}{6})=\frac{3}{5}$,则cosα=( )
| A. | $\frac{{3-4\sqrt{3}}}{10}$ | B. | $\frac{{3+4\sqrt{3}}}{10}$ | C. | $\frac{{-3-4\sqrt{3}}}{10}$ | D. | $\frac{{-3+4\sqrt{3}}}{10}$ |