题目内容
3．已知集合A={x|x2-x-2＜0}，$B=\left\{{x|{{log}_4}x＜\frac{1}{2}}\right\}$，则（ ）| A． | A∩B=∅ | B． | ∁UA∪B=R | C． | A∩B=B | D． | A∪B=B |
分析 根据不等式的性质求出集合A，B的等价条件，结合集合的基本运算进行判断即可．
解答 解：A={x|x2-x-2＜0}={x|-1＜x＜2}，$B=\left\{{x|{{log}_4}x＜\frac{1}{2}}\right\}$={x|0＜x＜4${\;}^{\frac{1}{2}}$}={x|0＜x＜2}，
则A∩B={x|0＜x＜2}=B，
故选：C
点评 本题主要考查集合的基本运算，求出集合的等价条件是解决本题的关键．
练习册系列答案
相关题目
7．对于函数y=f（x），部x与y的对应关系如下表：
数列{xn}满足x1=1，且对任意n∈N*，点（xn，xn+1）都在函数y=f（x）的图象上，则x1+x2+x3+x4+…+x2017+x2018的值为（ ）
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 3 | 7 | 5 | 9 | 6 | 1 | 8 | 2 | 4 |
| A． | 7560 | B． | 7564 | C． | 7550 | D． | 7554 |
14．已知f（x）是定义在R上的减函数，其导函数f'（x）满足$\frac{f（x）+xf'（x）}{f'（x）}＜1$，则下列结论中正确的是（ ）
| A． | f（x）＞0恒成立 | B． | f（x）＜0 | ||
| C． | 当且仅当x∈（-∞，1），f（x）＜0 | D． | 当且仅当x∈（1，+∞），f（x）＞0 |
11．设全集U=R，集合A={x|y=lgx}，B={x|x2-3x＞4}，则A∩（∁UB）=（ ）
| A． | {x|0≤x≤4} | B． | {x|-1≤x≤4} | C． | {x|-1≤x≤0} | D． | {x|0＜x≤4} |
18．定义在R上的奇函数f（x）满足f（2-x）=f（x），当x∈[0，1]时，f（x）=$\sqrt{x}$．又函数g（x）=cos$\frac{πx}{2}$，x∈[-3，3]，则函数F（x）=f（x）-g（x）的所有零点之和等于（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |
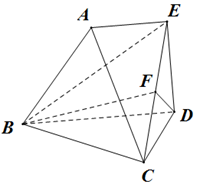如图所示，在多面体ABCDE中，△BCD是边长为2的正三角形，AE∥DB，AE⊥DE，2AE=BD，DE=1，面ABDE⊥面BCD，F是CE的中点．