题目内容
9．
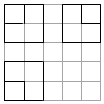如图，正方形网格中，粗实线画出的是某几何体的三视图，若该几何体的体积为7，则该几何体的表面积为（ ）| A． | 18 | B． | 21 | C． | 24 | D． | 27 |
分析 由三视图可知：该几何体为一个棱长为2x的正方体，在一个角去掉一个棱长为x的正方体余下的几何体．由该几何体的体积7=（2x）3-x3，解得x．即可得出表面积．
解答 
解：由三视图可知：该几何体为一个棱长为2x的正方体
在一个角去掉一个棱长为x的正方体，余下的几何体．
∴该几何体的体积7=（2x）3-x3，解得x=1．
∴该几何体的表面积=6×22=24．
故选：C．
点评 本题考查了正方体的三视图、面积和体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13．已知P为抛物线y2=4x上一个动点，Q为圆x2+（y-4）2=1上一个动点，当点P到点Q的距离与点P到抛物线的准线距离之和最小时，P点的横坐标为（ ）
| A． | $\frac{\sqrt{17}}{8}$ | B． | $\frac{9-\sqrt{17}}{8}$ | C． | $\frac{9}{8}$ | D． | $\sqrt{17}$ |
14．已知f（x）是定义在R上的减函数，其导函数f'（x）满足$\frac{f（x）+xf'（x）}{f'（x）}＜1$，则下列结论中正确的是（ ）
| A． | f（x）＞0恒成立 | B． | f（x）＜0 | ||
| C． | 当且仅当x∈（-∞，1），f（x）＜0 | D． | 当且仅当x∈（1，+∞），f（x）＞0 |
1．某中学有篮球社，吉他社，传统文化社，动漫社等多个社团，其中传统文化社借端午节来临之际举行包粽子送祝福活动，随机调查了高三50名男女生对粽子口味的喜好，统计如下表：
（1）按以上统计数据填写下面的2×2列联表，并运用独立性检验思想，判断是否有97.5%把握认为甜味粽和咸味粽的喜好与性别有关系？
参考公式及临界值表如下：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
（2）从被调查的50人中对玫瑰粽和什锦粽喜好的同学按照分层抽样的方法抽取4名同学按顺序进行深度调查，则前两位接受调查的都是喜好玫瑰粽同学的概率是多少？
| 甜味粽 | 咸味粽 | 南国风味 | ||||
| 枣子粽 | 豆沙粽 | 玫瑰粽 | 蛋黄粽 | 猪肉粽 | 什锦粽 | |
| 男生 | 4 | 3 | 1 | 10 | 4 | 3 |
| 女生 | 6 | 5 | 5 | 5 | 1 | 3 |
| 甜味粽 | 咸味粽 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18．定义在R上的奇函数f（x）满足f（2-x）=f（x），当x∈[0，1]时，f（x）=$\sqrt{x}$．又函数g（x）=cos$\frac{πx}{2}$，x∈[-3，3]，则函数F（x）=f（x）-g（x）的所有零点之和等于（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |