题目内容
12.设数列{an}的前n项和为Sn,a1=1,且对任意正整数n,点(an+1,Sn)都在直线2x+y-2=0上.(1)求数列{an}的通项公式;
(2)若bn=nan2,数列{bn}的前n项和为Tn,求证:Tn<$\frac{16}{9}$.
分析 (1)(an+1,Sn)都在直线2x+y-2=0上.可得2an+1+Sn-2=0,利用递推关系可得:an+1=$\frac{1}{2}{a}_{n}$.再利用等比数列的通项公式即可得出.
(2)bn=nan2=$n•(\frac{1}{4})^{n-1}$.再利用“错位相减法”与等比数列的求和公式即可得出.
解答 (1)解:(an+1,Sn)都在直线2x+y-2=0上.
∴2an+1+Sn-2=0,
∴n≥2时,2an+Sn-1-2=0,可得:2an+1-2an+an=0,∴an+1=$\frac{1}{2}{a}_{n}$.
∴数列{an}是等比数列,公比为$\frac{1}{2}$,首项为1.
∴an=$(\frac{1}{2})^{n-1}$.
(2)证明:bn=nan2=$n•(\frac{1}{4})^{n-1}$.
∴数列{bn}的前n项和为Tn=1+$2×\frac{1}{4}$+$3×(\frac{1}{4})^{2}$+…+$n•(\frac{1}{4})^{n-1}$,
∴$\frac{1}{4}{T}_{n}$=$\frac{1}{4}+2×(\frac{1}{4})^{2}$+…+(n-1)×$(\frac{1}{4})^{n-1}$+n$•(\frac{1}{4})^{n}$,
∴$\frac{3}{4}{T}_{n}$=$1+\frac{1}{4}$+$(\frac{1}{4})^{2}$+…+$(\frac{1}{4})^{n-1}$-n$•(\frac{1}{4})^{n}$=$\frac{1-(\frac{1}{4})^{n}}{1-\frac{1}{4}}$-n$•(\frac{1}{4})^{n}$,
∴Tn=$\frac{16}{9}$-$\frac{4+3n}{3×{4}^{n}}$<$\frac{16}{9}$.
点评 本题考查了数列递推关系、“错位相减法”、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | m>2 | B. | 0<m<1 | C. | m>0 | D. | m>1 |
| A. | y=±$\sqrt{7}$x | B. | y=±7x | C. | y=±$\frac{\sqrt{7}}{7}$x | D. | y=±$\frac{1}{7}$x |
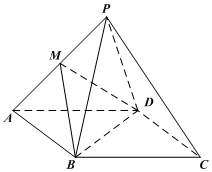 如图,在正四棱锥P-ABCD中,点M为侧棱PA的中点.
如图,在正四棱锥P-ABCD中,点M为侧棱PA的中点.