题目内容
关于x的方程ax2-|x|+a=0有四个不同的解，则实数a的值可能是（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
考点：根的存在性及根的个数判断
专题：计算题,函数的性质及应用
分析：分别把a=2，1，
，
代入方程ax2-|x|+a=0，验证即可．
| 1 |
| 2 |
| 1 |
| 4 |
解答：
解：若a=2，则2x2-|x|+2=0，△=1-16＜0，无解，
若a=1，则x2-|x|+1=0，△=1-4＜0，无解，
若a=
，则x2-2|x|+1=0，△=0，x=±1，
若a=
，则|x|2-4|x|+1=0，△＞0，方程有4个根，成立．
故选D．
若a=1，则x2-|x|+1=0，△=1-4＜0，无解，
若a=
| 1 |
| 2 |
若a=
| 1 |
| 4 |
故选D．
点评：本题考查了方程的根的个数的判断，属于基础题．
练习册系列答案
相关题目
已知异面直线a、b所成角为
，经过定点P与a、b所成的角均为
的平面有（ ）
| π |
| 3 |
| π |
| 6 |
| A、1个 | B、2个 | C、3个 | D、无数 |
设P为曲线C：y=x2+2x+3上点，且曲线C在点P处切线倾斜角的取值范围为[0，
]，则点P横坐标的取值范围为（ ）
| π |
| 4 |
A、[
| ||
| B、[-1，0] | ||
| C、[0，1] | ||
D、[-1，-
|
下列有关命题的说法正确的是（ ）
| A、命题“若α=β，则sinα=sinβ”的逆命题为真命题 | ||
| B、已知命题p：函数f（x）=tanx的定义域为{x|x≠kπ，k∈Z}，命题q：?x∈R，x2-x+1≥0；则命题p∧q为真命题 | ||
C、“a=2”是“直线y=-ax+2与直线y=
| ||
| D、命题“?x∈R，使得x2+2x+3＜0”的否定形式是真命题 |
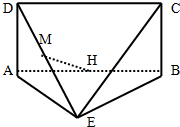已知平面ABCD⊥平面ABE，四边形ABCD是矩形，AD=AE=BE=2，M、H分别是DE、AB的中点，主（正）视图方向垂直平面ABCD时，左（侧）视图的面积为