题目内容
已知异面直线a、b所成角为
，经过定点P与a、b所成的角均为
的平面有（ ）
| π |
| 3 |
| π |
| 6 |
| A、1个 | B、2个 | C、3个 | D、无数 |
考点：平面与平面之间的位置关系
专题：空间角
分析：根据异面直线的定义和关系，进行判断即可得到结论．
解答：
解：过P作a'∥a，b'∥b，设直线a'、b'确定的平面为α
∵异面直线a、b成
，∴直线a'、b'所成锐角为
，
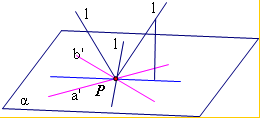钝角为
．
①当过P的平面经过钝角所在的角平分线且和α垂直时，a，b与平面所成的角都为
，满足条件；
②当过P的平面与平面α平行或重合时，此时两个平面的夹角为0，
当过P的平面与平面α垂直时，此时另个平面的夹角
，适当调整平面的位置，可使平面与a、b也都成
角，这样的平面有两个，
综上所述，过点P与a'、b'都成
角的平面有3个．
故选C
∵异面直线a、b成
| π |
| 3 |
| π |
| 3 |
钝角为| 2π |
| 3 |
①当过P的平面经过钝角所在的角平分线且和α垂直时，a，b与平面所成的角都为
| π |
| 6 |
②当过P的平面与平面α平行或重合时，此时两个平面的夹角为0，
当过P的平面与平面α垂直时，此时另个平面的夹角
| π |
| 2 |
| π |
| 6 |
综上所述，过点P与a'、b'都成
| π |
| 6 |
故选C
点评：本题主要考查直线和平面所成角的判断，根据空间异面直线和直线和平面的位置关系是解决本题的关键．
练习册系列答案
相关题目
函数f（x）=lg（x-1）+
的定义域是（ ）
| 3-x |
| A、（1，3） |
| B、[1，3] |
| C、（1，3] |
| D、[1，3） |
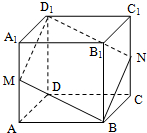在正方体ABCD-A1B1C1D1 中，过对角线BD1 的一个平面交AA1 于M，交CC1 于N．给出下列四个结论：
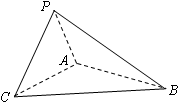如图，平面PAC⊥平面ABC，△PAC是正三角形，∠CAB=90°，AB=2AC．关于x的方程ax2-|x|+a=0有四个不同的解，则实数a的值可能是（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|