题目内容
一只口袋内装有大小相同的5只球,其中3只白球2只黑球,从中一次摸出两只球.
(1)共有多少个基本事件,并列出.
(2)摸出的两只球都是白球的概率.
(3)摸出的两只球是一黑一白的概率.
(1)共有多少个基本事件,并列出.
(2)摸出的两只球都是白球的概率.
(3)摸出的两只球是一黑一白的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:计算题,概率与统计
分析:(1)记白球为1,2,3号,黑球为4,5号,则(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).
(2)摸到两只白球:(1,2),(1,3),(2,3),故P=
.
(3)摸到两只球为一黑一白:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),故P=
.
(2)摸到两只白球:(1,2),(1,3),(2,3),故P=
| 3 |
| 10 |
(3)摸到两只球为一黑一白:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),故P=
| 3 |
| 5 |
解答:
解:(1)分别记白球为1,2,3号,黑球为4,5号,从中摸出2只球,有如下基本事件(摸到1,2号球用(1,2)表示)
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).
因此,共有10个基本事件.
(2),上述10个基本事件发生的可能性相同,且只有 3个基本事件是摸到两只白球(记为事件A),即(1,2),(1,3),(2,3),
故P(A)=
.
答:共有10个基本事件,摸出两只球都是白球的概率为
.
(3)上述10个基本事件发生的可能性相同,且只有 6个基本事件是摸到两只球为一黑一白(记为事件B),即(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),
故P(B)=
.
答:共有10个基本事件,摸出两只球都是白球的概率为
.
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5).
因此,共有10个基本事件.
(2),上述10个基本事件发生的可能性相同,且只有 3个基本事件是摸到两只白球(记为事件A),即(1,2),(1,3),(2,3),
故P(A)=
| 3 |
| 10 |
答:共有10个基本事件,摸出两只球都是白球的概率为
| 3 |
| 10 |
(3)上述10个基本事件发生的可能性相同,且只有 6个基本事件是摸到两只球为一黑一白(记为事件B),即(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),
故P(B)=
| 3 |
| 5 |
答:共有10个基本事件,摸出两只球都是白球的概率为
| 3 |
| 5 |
点评:本题考查了基本事件的列举与概率的求法,属于基础题.

练习册系列答案
相关题目
命题p:幂函数y=x3在(-∞,0)上单调递减;命题q:已知函数f(x)=x3-3x2+m,若a,b,c∈[1,3],且f(a),f(b),f(c)能构成一个三角形的三边长,则4<m<8.则下列说法正确的是( )
| A、p∧q为真命题 |
| B、p∧q为假命题 |
| C、(¬p)∧q为真命题 |
| D、p∧(¬q)为真命题 |
关于x的方程ax2-|x|+a=0有四个不同的解,则实数a的值可能是( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
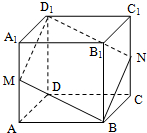 在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:
在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论: 如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x
如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x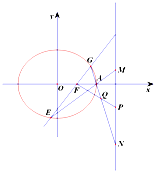 已知椭圆C:
已知椭圆C: