题目内容
下列有关命题的说法正确的是( )
| A、命题“若α=β,则sinα=sinβ”的逆命题为真命题 | ||
| B、已知命题p:函数f(x)=tanx的定义域为{x|x≠kπ,k∈Z},命题q:?x∈R,x2-x+1≥0;则命题p∧q为真命题 | ||
C、“a=2”是“直线y=-ax+2与直线y=
| ||
| D、命题“?x∈R,使得x2+2x+3<0”的否定形式是真命题 |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:A写出该命题的逆命题并判断真假性;
B判断命题p、q的真假性,从而得出p∧q的真假性;
C由a=2时,直线y=-ax+2与直线y=
x-1是否垂直判断充分性,
由直线y=-ax+2与直线y=
x-1垂直时,求出a的值,判断必要性;
D写出该命题的否定命题,再判断它的真假性.
B判断命题p、q的真假性,从而得出p∧q的真假性;
C由a=2时,直线y=-ax+2与直线y=
| a |
| 4 |
由直线y=-ax+2与直线y=
| a |
| 4 |
D写出该命题的否定命题,再判断它的真假性.
解答:
解:对于A,命题“若α=β,则sinα=sinβ”的逆命题是“若sinα=sinβ,则α=β”,
它是假命题,∴A错误;
对于B,∵函数f(x)=tanx的定义域为{x|x≠kπ+
,k∈Z},∴命题p错误,
x2-x+1=(x-
)2+
≥0,∴命题q正确,∴命题p∧q为假命题,B错误;
对于C,a=2时,直线y=-ax+2与直线y=
x-1垂直,充分性成立,
直线y=-ax+2与直线y=
x-1垂直时,-a•
=-1,解得a=±2,∴必要性不成立,
∴是充分不必要条件,C错误;
对于D,命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,x2+2x+3≥0”,
∵x2+2x+3=(x+1)2+2≥0,它是真命题,D正确.
故选:D.
它是假命题,∴A错误;
对于B,∵函数f(x)=tanx的定义域为{x|x≠kπ+
| π |
| 2 |
x2-x+1=(x-
| 1 |
| 2 |
| 3 |
| 4 |
对于C,a=2时,直线y=-ax+2与直线y=
| a |
| 4 |
直线y=-ax+2与直线y=
| a |
| 4 |
| a |
| 4 |
∴是充分不必要条件,C错误;
对于D,命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,x2+2x+3≥0”,
∵x2+2x+3=(x+1)2+2≥0,它是真命题,D正确.
故选:D.
点评:本题通过命题真假的判断,考查了四种命题之间的关系,复合命题真假的判断问题,直线的垂直判断问题以及命题的否定问题,是综合题.

练习册系列答案
相关题目
关于x的方程ax2-|x|+a=0有四个不同的解,则实数a的值可能是( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
命题“?x∈R,x2≥0”的否定为( )
| A、?x∈R,x2<0 |
| B、?x∈R,x2≥0 |
| C、?x∈R,x2<0 |
| D、?x∈R,x2≤0 |
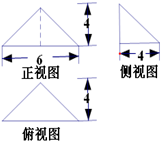 若某多面体的三视图(单位:cm),如图所示,其中正视图与俯视图均为等腰三角形,则此多面体的表面积是( )cm2.
若某多面体的三视图(单位:cm),如图所示,其中正视图与俯视图均为等腰三角形,则此多面体的表面积是( )cm2.A、5
| ||
B、32+12
| ||
| C、15 | ||
D、5+2
|
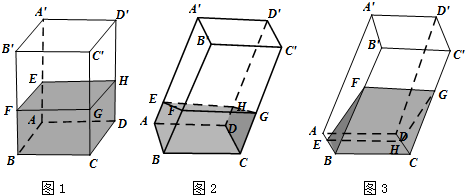
 如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x
如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x