题目内容
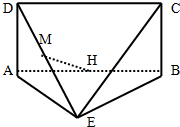 已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为
已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为| 2 |
(1)求证:MH∥平面BCE;
(2)求证:平面ADE⊥平面BCE.
考点:直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:对于第(1)问,思路1(由线线平行得线面平行):取CE的中点N,连接BN,只需证MH∥BN即可;思路2(由面面平行得线面平行):取AE的中点P,连接MP、HP,只需证明平面MPH∥平面BCE即可.
对于第(2)问,要证明面面垂直,由面面垂直的判定定理,可先证明平面BCE内的直线BE⊥平面ADE,问题转化为证BE⊥AE,BE⊥AD,根据已知条件及数据,设法探求BE与AE,及BE与AD的垂直关系即可证明.
对于第(2)问,要证明面面垂直,由面面垂直的判定定理,可先证明平面BCE内的直线BE⊥平面ADE,问题转化为证BE⊥AE,BE⊥AD,根据已知条件及数据,设法探求BE与AE,及BE与AD的垂直关系即可证明.
解答:
证明:(1)方法一:取CE的中点N,连接BN,如图1所示.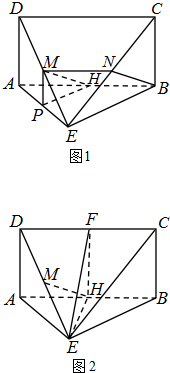
∵△CDE中,M、N分别是DE、CE的中点,∴MN∥CD且MN=
CD.
在矩形ABCD中,∵H是AB的中点,∴BH∥CD且BH=
CD,
∴MN∥BH且MN=BH,从而四边形BHMN为平行四边形,∴MH∥BN.
又∵MH?平面BCE,BN?平面BCE,∴MH∥平面BCE.
方法二:取AE的中点P,连接MP、HP,
在△ABE中,∵P、H分别是AE、AB的中点,∴HP∥BE,
∵HP?平面BCE,BE?平面BCE,∴HP∥平面BCE;同理有MP∥平面BCE,
又∵MP∩HP=P,∴平面MPH∥平面BCE,
∵MH?平面MPH,∴MH∥平面BCE.
(2)取CD中点F,连接EH、EF、FH,如图2所示,则在矩形ABCD中,FH⊥AB,FH=AD=2.
在△ABE中,AE=BE=2,∴EH⊥AB,∵FH∩EH=H,∴AB⊥平面EFH,
∵平面ABCD⊥平面ABE,∴∠EHF=90°,
∴Rt△EFH的面积等于几何体E-ABCD左(侧)视图的面积,
得
EH×FH=
EH×2=
,即EH=
,
∴在ABE中,有AH2+EH2=BH2+EH2=AE2=DE2=22,得AH=BH=
,从而AB=2
.
由AE2+BE2=AB2=8知,AE⊥BE.
∵平面ABCD⊥平面ABE,四边形ABCD是矩形,∴AD⊥平面ABE,
又∵BE?平面ABE,∴AD⊥BE,而AD∩AE=A,∴BE⊥平面ADE,
∵BE?平面BCE,∴平面ADE⊥平面BCE.

∵△CDE中,M、N分别是DE、CE的中点,∴MN∥CD且MN=
| 1 |
| 2 |
在矩形ABCD中,∵H是AB的中点,∴BH∥CD且BH=
| 1 |
| 2 |
∴MN∥BH且MN=BH,从而四边形BHMN为平行四边形,∴MH∥BN.
又∵MH?平面BCE,BN?平面BCE,∴MH∥平面BCE.
方法二:取AE的中点P,连接MP、HP,
在△ABE中,∵P、H分别是AE、AB的中点,∴HP∥BE,
∵HP?平面BCE,BE?平面BCE,∴HP∥平面BCE;同理有MP∥平面BCE,
又∵MP∩HP=P,∴平面MPH∥平面BCE,
∵MH?平面MPH,∴MH∥平面BCE.
(2)取CD中点F,连接EH、EF、FH,如图2所示,则在矩形ABCD中,FH⊥AB,FH=AD=2.
在△ABE中,AE=BE=2,∴EH⊥AB,∵FH∩EH=H,∴AB⊥平面EFH,
∵平面ABCD⊥平面ABE,∴∠EHF=90°,
∴Rt△EFH的面积等于几何体E-ABCD左(侧)视图的面积,
得
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴在ABE中,有AH2+EH2=BH2+EH2=AE2=DE2=22,得AH=BH=
| 2 |
| 2 |
由AE2+BE2=AB2=8知,AE⊥BE.
∵平面ABCD⊥平面ABE,四边形ABCD是矩形,∴AD⊥平面ABE,
又∵BE?平面ABE,∴AD⊥BE,而AD∩AE=A,∴BE⊥平面ADE,
∵BE?平面BCE,∴平面ADE⊥平面BCE.
点评:1.本题考查了几何的三视图,线面平行的判定定理,面面垂直的判定定理等,考查知识点较多,且综合性强,利用已知数据及线、面位置关系进行合理地推理是关键.
2.事实上,第(1)问还可以连结FM,要证MH∥平面BCE,只需证平面MFH∥平面BCE,由FH∥BC及MF∥CE得证;第(2)问也可以利用向量法:以H为坐标原点,射线HE为x轴,射线HB为y轴,射线HF为z轴建立空间直角坐标系,分别找到平面ADE与平面BCE的法向量,问题转化为证明这两个法向量互相垂直,只需通过计算得出其数量积为零即可.
2.事实上,第(1)问还可以连结FM,要证MH∥平面BCE,只需证平面MFH∥平面BCE,由FH∥BC及MF∥CE得证;第(2)问也可以利用向量法:以H为坐标原点,射线HE为x轴,射线HB为y轴,射线HF为z轴建立空间直角坐标系,分别找到平面ADE与平面BCE的法向量,问题转化为证明这两个法向量互相垂直,只需通过计算得出其数量积为零即可.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
命题p:幂函数y=x3在(-∞,0)上单调递减;命题q:已知函数f(x)=x3-3x2+m,若a,b,c∈[1,3],且f(a),f(b),f(c)能构成一个三角形的三边长,则4<m<8.则下列说法正确的是( )
| A、p∧q为真命题 |
| B、p∧q为假命题 |
| C、(¬p)∧q为真命题 |
| D、p∧(¬q)为真命题 |
关于x的方程ax2-|x|+a=0有四个不同的解,则实数a的值可能是( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
若函数f(x)=|ax|-x-a(a>0)有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
如果椭圆
+y2=k上两点间的距离最大值为8,则k的值为( )
| x2 |
| 4 |
| A、32 | B、16 | C、8 | D、4 |
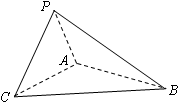 如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.
如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.