题目内容
从集合{1,2,4,8,16,32,64}的所有非空真子集中等可能地取出一个.
(I)求所取的子集中元素从小到大排列成等比数列的概率;
(Ⅱ)记所取出的子集的元素个数为ξ,求ξ的分布列和数学期望.
(I)求所取的子集中元素从小到大排列成等比数列的概率;
(Ⅱ)记所取出的子集的元素个数为ξ,求ξ的分布列和数学期望.
考点:离散型随机变量及其分布列,古典概型及其概率计算公式,离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:(I)确定所有非空真子集、所取的子集中元素从小到大排列成等比数列的个数,利用古典概型概率公式可求概率;
(Ⅱ)ξ的可能取值是1、2、3、4、5、6,求出相应的概率,可得ξ的分布列和数学期望.
(Ⅱ)ξ的可能取值是1、2、3、4、5、6,求出相应的概率,可得ξ的分布列和数学期望.
解答:
解:(I)集合{1,2,4,8,16,32,64}的所有非空真子集,共有n=27-2=126,
符合条件的子集有:三元集9个,四元集5个,五元集3个,六元集2个,共有m=9+5+3+2=19个,
∴所求概率为P=
=
;
(Ⅱ)ξ的可能取值是1、2、3、4、5、6,
P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
,
P(ξ=4)=
=
,P(ξ=5)=
=
,P(ξ=6)=
=
,
∴ξ的分布列
数学期望Eξ=1×
+2×
+3×
+4×
+5×
+6×
=
=
.
符合条件的子集有:三元集9个,四元集5个,五元集3个,六元集2个,共有m=9+5+3+2=19个,
∴所求概率为P=
| m |
| n |
| 19 |
| 126 |
(Ⅱ)ξ的可能取值是1、2、3、4、5、6,
P(ξ=1)=
| ||
| 126 |
| 7 |
| 126 |
| ||
| 126 |
| 21 |
| 126 |
| ||
| 126 |
| 35 |
| 126 |
P(ξ=4)=
| ||
| 126 |
| 35 |
| 126 |
| ||
| 126 |
| 21 |
| 126 |
| ||
| 126 |
| 7 |
| 126 |
∴ξ的分布列
| ξ | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||
| P |
|
|
|
|
|
|
| 7 |
| 126 |
| 21 |
| 126 |
| 35 |
| 126 |
| 35 |
| 126 |
| 21 |
| 126 |
| 7 |
| 126 |
| 441 |
| 126 |
| 7 |
| 2 |
点评:本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.本题还考到了集合的子集个数问题,一个含有n个元素的集合的子集个数是2n.

练习册系列答案
相关题目
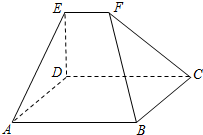 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.