题目内容
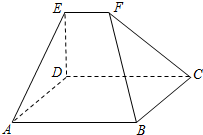 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF;
(3)若AB=4,AD=EF=ED=2,CF中点为M,求直线ED与平面MBD所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的性质,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由四边形ABCD是矩形,得到AB∥平面CDEF,由此能证明AB∥EF.
(2)由已知条件推导出DE⊥BC,从而得到BC⊥平面CDEF,由此能证明平面BCF⊥平面CDEF.
(3)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出直线ED与平面MBD所成角的正弦值.
(2)由已知条件推导出DE⊥BC,从而得到BC⊥平面CDEF,由此能证明平面BCF⊥平面CDEF.
(3)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出直线ED与平面MBD所成角的正弦值.
解答:
(1)证明:∵四边形ABCD是矩形,∴AB∥CD,
∵AB不包含于平面CDEF,CD?平面CDEF,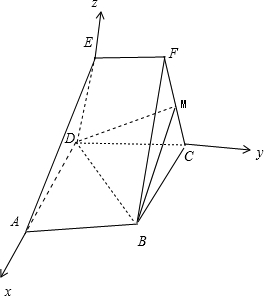
∴AB∥平面CDEF.…(4分)
∵AB?平面ABFE,平面ABFE∩平面CDEF=EF,
∴AB∥EF..…(5分)
(2)证明:∵DE⊥平面ABCD,BC?平面ABCD,
∴DE⊥BC..…(7分)
∵BC⊥CD,CD∩DE=D,CD,DE?平面CDEF,
∴BC⊥平面CDEF.…(8分)
∵BC?平面BCF,∴平面BCF⊥平面CDEF.…(9分)
(3)解:以D为原点,DA为x轴,DC为y轴,DE为z轴,
建立空间直角坐标系,.…(10分)
∵AB=4,AD=EF=ED=2,CF中点为M,
∴D(0,0,0),E(0,0,2),F(0,2,2),
C(0,4,0),M(0,3,1),B(2,4,0),
∴
=(0,0,2),
=(0,3,1),
=(2,4,0),
设平面MBD的法向量
=(x,y,z),
则
,取x=2,得
=(2,-1,3),…(12分)
设直线ED与平面MBD所成角为θ,
则sinθ=|cos<
,
>|=|
|=
.
∴直线ED与平面MBD所成角的正弦值为
.…(13分)
∵AB不包含于平面CDEF,CD?平面CDEF,

∴AB∥平面CDEF.…(4分)
∵AB?平面ABFE,平面ABFE∩平面CDEF=EF,
∴AB∥EF..…(5分)
(2)证明:∵DE⊥平面ABCD,BC?平面ABCD,
∴DE⊥BC..…(7分)
∵BC⊥CD,CD∩DE=D,CD,DE?平面CDEF,
∴BC⊥平面CDEF.…(8分)
∵BC?平面BCF,∴平面BCF⊥平面CDEF.…(9分)
(3)解:以D为原点,DA为x轴,DC为y轴,DE为z轴,
建立空间直角坐标系,.…(10分)
∵AB=4,AD=EF=ED=2,CF中点为M,
∴D(0,0,0),E(0,0,2),F(0,2,2),
C(0,4,0),M(0,3,1),B(2,4,0),
∴
| DE |
| DM |
| DB |
设平面MBD的法向量
| n |
则
|
| n |
设直线ED与平面MBD所成角为θ,
则sinθ=|cos<
| DE |
| n |
| 6 | ||
2
|
3
| ||
| 28 |
∴直线ED与平面MBD所成角的正弦值为
3
| ||
| 28 |
点评:本题考查直线平行的证明,考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=
四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD= 某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表: