题目内容

已知tanθ=
1
2
，求θ．
考点：反三角函数的运用
专题：计算题,三角函数的求值
分析：由tanθ=
1
2
，结合正切函数的周期性，即可得出结论．
解答： 解：∵tanθ=
1
2
，
∴θ=kπ+arctan
1
2
，k∈Z．
点评：本题考查反三角函数的运用，考查正切函数的周期性，比较基础．
练习册系列答案
相关题目
已知数列{log2（an-1）}（n∈N*）为等差数列，且a1=3，a2=5．
（1）求{an}的通项公式．
（2）求
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
关于n的表达式．
若焦距为4的双曲线的两条渐近线互相垂直，则此双曲线的实轴长为（　　）
A、4
2
B、2
2
C、4
D、2
已知AB是圆O的直径，P是上半圆上的任意一点，PC是∠APB的平分线，E是下半圆的中点．
求证：直线PC经过点E．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点分别为F1，F2，过点F2作双曲线C的一条渐近线的垂线，垂足为H，交双曲线于点M且
F2M
=2
MH
，则双曲线C的离心率为
 
．
在“由于任何数的平方都是非负数，所以（2i）2≥0”这一推理中，产生错误的原因是（　　）
A、推理的形式不符合三段论的要求
B、大前提错误
C、小前提错误
D、推理的结果错误
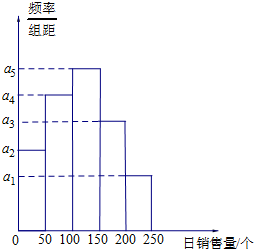广州某商场根据以往某种商品的销售记录，绘制了日销售量的频率分布表（如表）和频率分布直方图（如图）． 
分组频数频率
[0，50]n10.15
（50，100]n20.25
（100，150]n30.30
（150，200]n40.20
（200，250]n50.10
将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．
（1）求a1，a3的值．
（2）求在未来连续3天里，有连续2天的日销售量都高于100个且另1天的日销售量不高于50个的概率；
（3）用X表示在未来3天里日销售量高于100个的天数，求随机变量X的分布列和数学期望．
若函数f（x）=
1
x
，则
∫
e
1
f（x）dx=
 
．
若实数x，y满足
x-y+2≥0
x+y≥0
x≤1
，则z=3x+y的最小值是（　　）
A、-4B、-2C、2D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网