题目内容
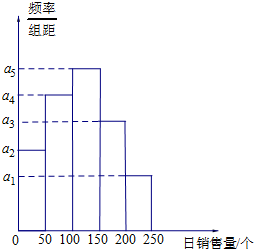 广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图). | 分组 | 频数 | 频率 |
| [0,50] | n1 | 0.15 |
| (50,100] | n2 | 0.25 |
| (100,150] | n3 | 0.30 |
| (150,200] | n4 | 0.20 |
| (200,250] | n5 | 0.10 |
(1)求a1,a3的值.
(2)求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50个的概率;
(3)用X表示在未来3天里日销售量高于100个的天数,求随机变量X的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由频率分布直方图,能求出a1,a3的值.
(2)设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,B表示事件“在未来连续3天里有连续2天日销售量高于100个且另1天销售量不高于50个”,由此能求出结果.
(3)X的可能取值为0,1,2,3,且X~B(3,0.6),由此能求出X的分布列和EX.
(2)设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,B表示事件“在未来连续3天里有连续2天日销售量高于100个且另1天销售量不高于50个”,由此能求出结果.
(3)X的可能取值为0,1,2,3,且X~B(3,0.6),由此能求出X的分布列和EX.
解答:
(本小题满分12分)
(1)解:由频率分布直方图,得:
a1=
=0.002,a3=
=0.004.…(2分)
(2)解:设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,
B表示事件“在未来连续3天里有连续2天日销售量高于100个且另1天销售量不高于50个”.
P(A1)=0.30+0.20+0.10=0.6,P(A2)=0.15,
故所求概率:P(B)=0.6×0.6×0.15×2=0.108.…(5分)
(3)解:依题意,X的可能取值为0,1,2,3,且X~B(3,0.6).…(6分)
P(X=0)=
•(1-0.6)3=0.064,
P(X=1)=
×0.6×(1-0.6)2=0.288,
P(X=2)=
×0.62×(1-0.6)=0.432,
P(X=3)=
×0.63=0.216,…(10分)
∴X的分布列为
…(11分)
∴EX=3×0.6=1.8.…(12分)
(1)解:由频率分布直方图,得:
a1=
| 0.10 |
| 50 |
| 0.20 |
| 50 |
(2)解:设A1表示事件“日销售量高于100个”,A2表示事件“日销售量不高于50个”,
B表示事件“在未来连续3天里有连续2天日销售量高于100个且另1天销售量不高于50个”.
P(A1)=0.30+0.20+0.10=0.6,P(A2)=0.15,
故所求概率:P(B)=0.6×0.6×0.15×2=0.108.…(5分)
(3)解:依题意,X的可能取值为0,1,2,3,且X~B(3,0.6).…(6分)
P(X=0)=
| C | 0 3 |
P(X=1)=
| C | 1 3 |
P(X=2)=
| C | 2 3 |
P(X=3)=
| C | 3 3 |
∴X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
∴EX=3×0.6=1.8.…(12分)
点评:本题考查频率分布直方图的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
已知集合A={x|x>0},B={x|
<0},则A∩B等于( )
| x |
| x-1 |
| A、(0,1) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
下列函数中,既是偶函数,又在(0,+∞)上是单调减函数的是( )
A、y=x
| ||
| B、y=cosx | ||
| C、y=ln|x+1| | ||
| D、y=-2|x| |
若函数f(x)=cos2x+asinx在区间(
,
)是减函数,则a的取值范围是( )
| π |
| 6 |
| π |
| 2 |
| A、(2,4) |
| B、(-∞,2] |
| C、(-∞,4] |
| D、[4,+∞) |