题目内容
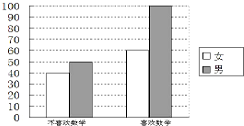为考察高中生的性别与喜欢数学课程之间的关系，在某学校高中生中随机抽取了250名学生，得到如图的二维条形图．（1）根据二维条形图，完形填空2×2列联表：
| 男 | 女 | 合计 | |
| 喜欢数学课程 | |||
| 不喜欢数学课程 | |||
| 合计 |
考点：独立性检验的应用,频率分布直方图
专题：计算题,概率与统计
分析：（1）根据所给的二维条形图看出喜欢数学课程和不喜欢数学课程的学生数，得到列联表．
（2）把列联表中的数据代入求观测值的公式，求出这组数据的观测值，把观测值同临界值进行比较，得到有60%的把握认为“性别与喜欢数学有关系”．
（2）把列联表中的数据代入求观测值的公式，求出这组数据的观测值，把观测值同临界值进行比较，得到有60%的把握认为“性别与喜欢数学有关系”．
解答：
解：（1）
（2）K2=
≈1.16＞0.708，
∴有60%的把握认为“性别与喜欢数学有关系”．
| 男 | 女 | 合 计 | |
| 喜欢数学课程 | 100 | 60 | 160 |
| 不喜欢数学课程 | 50 | 40 | 90 |
| 合 计 | 150 | 100 | 250 |
| 25(100×40-60×50)2 |
| 160×90×150×100 |
∴有60%的把握认为“性别与喜欢数学有关系”．
点评：本题考查独立性检验的应用，本题解题的关键是正确读图和作图，正确理解临界值对应的概率的意义，本题是一个基础题．
练习册系列答案
相关题目
一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则事件A与B同时发生的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=2x2-lnx的递减区间是（ ）
A、（0，
| ||||
B、（-
| ||||
C、（
| ||||
D、（-∞，-
|
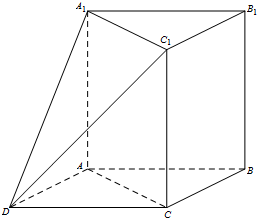如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1． 
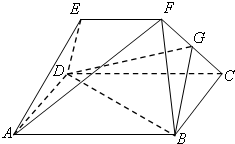如图几何体中，四边形ABCD为矩形，AB=2BC=4，BF=CF=AE=DE，EF=2，EF∥AB，AF⊥CF．