题目内容

已知V1=
△x
t1
，a=
2△x(t1-t2)
t1t2(t1+t2)
，化简可得V1=V0+a
t1
2
，求V0的表达式．
考点：进行简单的演绎推理
专题：计算题
分析：由已知中V1=
△x
t1
，a=
2△x(t1-t2)
t1t2(t1+t2)
，V1=V0+a
t1
2
，可得：V0=
△x
t1
-
2△x(t1-t2)
t1t2(t1+t2)
•
t1
2
，整理可得答案．
解答： 解：∵V1=
△x
t1
，a=
2△x(t1-t2)
t1t2(t1+t2)
，V1=V0+a
t1
2
，
∴
△x
t1
=V0+
2△x(t1-t2)
t1t2(t1+t2)
•
t1
2
，
∴V0=
△x
t1
-
2△x(t1-t2)
t1t2(t1+t2)
•
t1
2
=
△x
t1
-
△x(t1-t2)
t2(t1+t2)
=
△x[t2(t1+t2)-t1(t1-t2)]
t1t2(t1+t2)
点评：本题考查的学生的计算能力，难度不大，直接代入化简即可得到答案．
练习册系列答案
相关题目
已知函数f（x）=loga（1-ax）（0＜a＜1），若f（x）＞1，求x的取值范围．
若函数y=lg[（a2-1）x2+（a-1）x+1]的定义域为R，则实数a的取值范围是
 
．
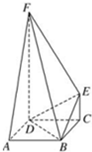如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．
（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=
3
，EF=2
3
，则另一边BC的长为何值时，三棱锥F-BDE的体积为
3
．
已知△ABC中，∠B=
π
3
，b=2
3
，求；
（1）三角形面积的最大值；
（2）a+c的取值范围．
求下列函数的值域：
（1）y=（
2
3
）-|x|；
（2）y=2
1
x-4
的值域．
已知函数f（x）=x2，值域为{1，4}时定义域为
 
．
已知f（x）是定义域在（-1，1）上的奇函数，当x∈（0，1）时，f（x）=
2x
4x+1
，求f（x）在（-1，1）上的解析式．
面面垂直的判定定理：文字语言：
 
；符号语言：
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网