题目内容
已知函数f（x）=loga（1-ax）（0＜a＜1），若f（x）＞1，求x的取值范围．
考点：复合函数的单调性
专题：导数的概念及应用
分析：由真数大于0求出原函数的定义域，然后由a的范围结合对数函数的单调性转化为一次不等式求出a的范围，最后取交集得答案．
解答：
解：由1-ax＞0，得ax＜1，
而a＞0，
∴x＜
，即定义域为（-∞，
），
∵0＜a＜1，
由f（x）＞1，得1-ax＜a，解得：x＞
-1．
综上，x的取值范围是(
-1，
)．
而a＞0，
∴x＜
| 1 |
| a |
| 1 |
| a |
∵0＜a＜1，
由f（x）＞1，得1-ax＜a，解得：x＞
| 1 |
| a |
综上，x的取值范围是(
| 1 |
| a |
| 1 |
| a |
点评：本题考查了复合函数的单调性，考查了对数不等式的解法，关键是注意对数函数的定义域，是中档题．
练习册系列答案
口算能手系列答案
相关题目
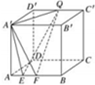如图，正方体ABCD-A′B′C′D′的棱长为4，动点E，F在棱AB上，且EF=2，动点Q在棱D′C′上，则三棱锥A′-EFQ的体积（ ）| A、与点E，F位置有关 |
| B、与点Q位置有关 |
| C、与点E，F，Q位置有关 |
| D、与点E，F，Q位置均无关，是定值 |
在正四棱锥S-ABCD中，SA=