Question

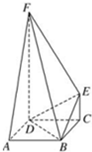如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．
（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=

3

，EF=2

3

，则另一边BC的长为何值时，三棱锥F-BDE的体积为

3

．

Answer 1

考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（1）过点E作EM∥CD，交FD于M，连接AM，结合题意得AB∥EM且AB=EM，所以四边形ABEM是平行四边形，得BE∥AM，从而得到BE∥平面ADF；
（2）算出Rt△DEF中DE、DF的长，从而得到Rt△DEF的面积．再以B为顶点、△DEF为底面，得V_B-DEF=

1

3

S_△DEF×BC，用等体积转换得V_B-DEF=V_F-BDE=

3

，从而算出BC的长，得三棱锥F-BDE的体积．

解答： 解：（1）证明：过点E作EM∥CD，交FD于M，连接AM
∵CE∥DF，EM∥CD，∴四边形CEMD是平行四边形．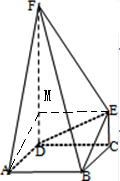
由此可得EM∥CD且EM=CD
∵AB∥CD且AB=CD，
∴AB∥EM且AB=EM，
∴四边形ABEM是平行四边形，
∴BE∥AM，
∵BE?平面ADF，AM?平面ADF，
∴BE∥平面ADF；
（2）由EF=2

3

，EM=AB=

3

，得FM=3且∠EFM=30°，
由∠DEF=90°，可得FD=4，从而DE=2
∵BC⊥CD，BC⊥DF，CD∩DF=D，∴BC⊥平面CDEF
∴V_F-BDE=V_B-DEF=

1

3

S_△DEF×BC
∵S_△DEF=

1

2

×DE×EF=2

3

，V_F-BDE=

3

，
∴BC=

3VF-BDE

S△DEF

=

3 3

2 3

=

3

2

综上所述，当BC=

3

2

时，三棱锥F-BDE的体积为

3

．

点评：本题考查了线面平行的判断以及三棱锥体积的运用，属于基础题．