题目内容
设关于x,y的不等式组
表示的平面区域内存在点P(a,b),满足a-3b=4,则实数m的取值范围是( )
|
| A、(-∞,1) |
| B、(-∞,1] |
| C、(-∞,-1) |
| D、(-∞,-1] |
考点:简单线性规划
专题:不等式的解法及应用
分析:先根据约束条件
画出可行域.要使可行域存在点P(a,b),满足a-3b=4,必有m<-3m+4,要求可行域包含直线y=
x-1上的点,只要边界点(-m,1-2m)在直线y=
x-
的上方,且(-m,m)在直线y=
x-
的下方,从而建立关于m的不等式组,解之可得答案.
|
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
解答:
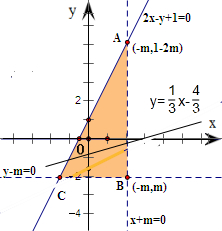 解:约束条件
解:约束条件
不是的可行域如图,
要使可行域存在点P(a,b),满足a-3b=4,必有m<-3m+4,要求可行域包含直线y=
x-
上的点,只要边界点(-m,1-2m)
在直线y=
x-
的上方,且(-m,m)在直线y=
x-
的下方,
故得不等式组
,
解之得:m<-1.
故选:C.
 解:约束条件
解:约束条件
|
要使可行域存在点P(a,b),满足a-3b=4,必有m<-3m+4,要求可行域包含直线y=
| 1 |
| 3 |
| 4 |
| 3 |
在直线y=
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
故得不等式组
|
解之得:m<-1.
故选:C.
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知曲线y=
-3lnx的一条切线的斜率为2,则切点的横坐标为( )
| x2 |
| 2 |
| A、3 | ||
| B、2 | ||
| C、1 | ||
D、
|
2
,(
)-1,3
的大小顺序为( )
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
A、3
| ||||||
B、2
| ||||||
C、(
| ||||||
D、2
|
正三棱锥S-ABC中,若侧棱 SA=4
,高SO=4,则此正三棱锥S-ABC外接球的表面积是( )
| 3 |
| A、36π | B、64π |
| C、144π | D、256π |
 用边长为6分米的正方形铁皮做一个无盖的水箱,先在四角分别截去一个小正方形,然后把四边翻转90°,再焊接而成(如图).设水箱底面边长为x分米,则( )
用边长为6分米的正方形铁皮做一个无盖的水箱,先在四角分别截去一个小正方形,然后把四边翻转90°,再焊接而成(如图).设水箱底面边长为x分米,则( )| A、水箱容积最大为8立方分米 |
| B、水箱容积最大为64立方分米 |
| C、当x在(0,3)时,水箱容积V(x)随x增大而增大 |
| D、当x在(0,3)时,水箱容积V(x)随x增大而减小 |



