题目内容
在公差不为0的等差数列{an}中,a1=-12,且a8,9,a11依次成等差数列.
(Ⅰ)求数列{an}的公差;
(Ⅱ)设Sn为数列{an}的前n项和,求Sn的最小值,并求出此时的n值.
(Ⅰ)求数列{an}的公差;
(Ⅱ)设Sn为数列{an}的前n项和,求Sn的最小值,并求出此时的n值.
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ)由已知得a1=-12,(a1+8d)2=(a1+7d)(a1+10d),由此能求出数列{an}的公差d.
(Ⅱ)由(Ⅰ)知Sn=-12n+n(n-1)=n2-13n=(n-
)2-
,由此能求出Sn的最小值及此时的n值.
(Ⅱ)由(Ⅰ)知Sn=-12n+n(n-1)=n2-13n=(n-
| 13 |
| 2 |
| 169 |
| 4 |
解答:
解:(Ⅰ)∵公差不为0的等差数列{an}中,
a1=-12,且a8,9,a11依次成等差数列,
∴(a1+8d)2=(a1+7d)(a1+10d),
整理,得a1=-6d,解得d=2.
∴数列{an}的公差d=2.
(Ⅱ)由(Ⅰ)知Sn=-12n+n(n-1)=n2-13n,
∵n2-13n=(n-
)2-
,且n∈N+,
∴当n=6或n=7时,
Sn取最小值S6=S7=-42.
a1=-12,且a8,9,a11依次成等差数列,
∴(a1+8d)2=(a1+7d)(a1+10d),
整理,得a1=-6d,解得d=2.
∴数列{an}的公差d=2.
(Ⅱ)由(Ⅰ)知Sn=-12n+n(n-1)=n2-13n,
∵n2-13n=(n-
| 13 |
| 2 |
| 169 |
| 4 |
∴当n=6或n=7时,
Sn取最小值S6=S7=-42.
点评:本题考查等差数列的公差的求法,考查Sn的最小值及此时的n值的求法,解题时要注意等差数列的性质的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
将棱长为a 的正方体ABCD-A1B1C1D1沿截面DA1C1截去一个角后,剩下的几何体体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
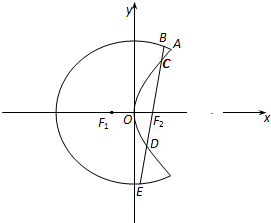 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”.若|AF1|=7,|AF2|=5.
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”.若|AF1|=7,|AF2|=5.