题目内容
已知数列{an}的前n项和为Sn,且满足Sn=2an-n,(n∈N*)
(1)求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn,求满足不等式
≥128的最小n值.
(1)求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn,求满足不等式
| Tn-2 |
| 2n-1 |
考点:数列与不等式的综合,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)运用等比数列的公式性质求解,
(2)运用求和公式列出来,再用错位相减的方法求出数列的和,最后解不等式确定n的范围,及最小值.
(2)运用求和公式列出来,再用错位相减的方法求出数列的和,最后解不等式确定n的范围,及最小值.
解答:
解:(1)因为Sn=2an-n,
所以Sn-1=2an-1-(n-1),(n≥2,n∈N*),
两式相减得an=2an-1+1,
所以an+1=2(an-1+1),(n≥2,n∈N*),
又因为a1+1=2,所以{an+1}是首项为2,公比为2的等比数列,
所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,
所以bn=(2n+1)•2n
可以得到:Tn=3×2+5×22+7×23+…+(2n-1)•2n-1+(2n+1)•2n,①
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,②
①-②得:-Tn=3×2+2(22+23+ …+2n)-(2n+1)•2n+1
=6+2×
-(2n+1)•2n+1
=-2+2n+2-(2n+1)•2n+1
=-2-(2n-1)•2n+1,
所以Tn=2+(2n-1)•2n+1
若
≥128,
则
≥128,
即2^n+1,所以n+1≥7,解得n≥6,
所以满足不等式
≥128,的最小n值6,
所以Sn-1=2an-1-(n-1),(n≥2,n∈N*),
两式相减得an=2an-1+1,
所以an+1=2(an-1+1),(n≥2,n∈N*),
又因为a1+1=2,所以{an+1}是首项为2,公比为2的等比数列,
所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,
所以bn=(2n+1)•2n
可以得到:Tn=3×2+5×22+7×23+…+(2n-1)•2n-1+(2n+1)•2n,①
2Tn=3×22+5×23+…+(2n-1)•2n+(2n+1)•2n+1,②
①-②得:-Tn=3×2+2(22+23+ …+2n)-(2n+1)•2n+1
=6+2×
| 22-2n×2 |
| 1-2 |
=-2+2n+2-(2n+1)•2n+1
=-2-(2n-1)•2n+1,
所以Tn=2+(2n-1)•2n+1
若
| Tn-2 |
| 2n-1 |
则
| 2+(2n-1)•2n+1-2 |
| 2n-1 |
即2^n+1,所以n+1≥7,解得n≥6,
所以满足不等式
| Tn-2 |
| 2n-1 |
点评:本题考查了数列的概念公式,错位相减求和,综合不等式解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各组函数表示相等函数的是( )
A、y=
| |||
B、y=
| |||
| C、y=x0与 y=1 | |||
D、y=
|
直线
x+y-2
=0的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
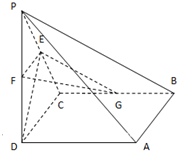 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.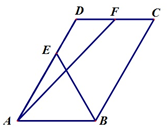 已知平行四边形ABCD中,|
已知平行四边形ABCD中,|