题目内容
已知函数f(x)=-
x3+4x-4.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)求函数f(x)在区间[-1,3]上的最值.
| 1 |
| 3 |
(Ⅰ)求函数f(x)的极值;
(Ⅱ)求函数f(x)在区间[-1,3]上的最值.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)由已知得f'(x)=-x2+4,由此利用导数性质能求出函数f(x)的极值.
(Ⅱ)求出f(-1)=-
,f(2)=
,f(3)=-1,由此能求出函数f(x)在区间[-1,3]上的最值.
(Ⅱ)求出f(-1)=-
| 23 |
| 3 |
| 4 |
| 3 |
解答:
(本小题共14分)
解:(Ⅰ)由f(x)=-
x3+4x-4.
得f'(x)=-x2+4…3
令f'(x)=0解得x1=-2,x2=2
列表:
所以当x=-2时,函数f(x)有极小值-
;
当x=2时函数f(x)有极大值
.…9
(Ⅱ)因为f(-1)=-
,
f(2)=
f(3)=-1,
所以函数f(x)在区间[-1,3]上的最大值是
,最小值是-
.…14
解:(Ⅰ)由f(x)=-
| 1 |
| 3 |
得f'(x)=-x2+4…3
令f'(x)=0解得x1=-2,x2=2
列表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f'(x) | - | + | - | ||
| f(x) | 减 | 极小值 | 增 | 极大值 | 减 |
| 28 |
| 3 |
当x=2时函数f(x)有极大值
| 4 |
| 3 |
(Ⅱ)因为f(-1)=-
| 23 |
| 3 |
f(2)=
| 4 |
| 3 |
所以函数f(x)在区间[-1,3]上的最大值是
| 4 |
| 3 |
| 23 |
| 3 |
点评:本题主要考查极值的概念、利用导数研究函数的单调性等基础知识,同时考查推理论证能力,分类讨论等综合解题能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
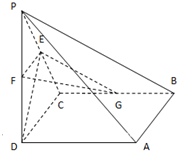 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.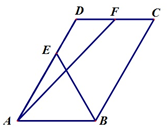 已知平行四边形ABCD中,|
已知平行四边形ABCD中,|