Question

将棱长为a 的正方体ABCD-A₁B₁C₁D₁沿截面DA₁C₁截去一个角后，剩下的几何体体积为（　　）

• A、

  a3

  2

• B、

  2a3

  3

• C、

  3a3

  4

• D、

  5a3

  6

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：正方体ABCD-A₁B₁C₁D₁的体积V=a³，VD1-A1DC1=VC1-A1DD1=

1

3

×a×

1

2

a×a=

1

6

a3．由此能求出将棱长为a 的正方体ABCD-A₁B₁C₁D₁沿截面DA₁C₁截去一个角后，剩下的几何体体积．

解答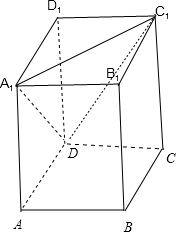： 解：棱长为a 的正方体ABCD-A₁B₁C₁D₁中，
正方体ABCD-A₁B₁C₁D₁的体积V=a³，
VD1-A1DC1=VC1-A1DD1=

1

3

×C1D1×S△A1DD1=

1

3

×a×

1

2

a×a=

1

6

a3．
∴将棱长为a 的正方体ABCD-A₁B₁C₁D₁沿截面DA₁C₁截去一个角后，
剩下的几何体体积为：a3-

1

6

a3=

5

6

a3．
故选：D．

点评：本题考查空间几何体的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．