题目内容
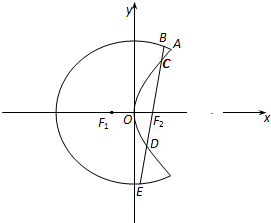如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．（Ⅰ）求曲线C1和C2所在的椭圆和抛物线方程；
（Ⅱ）过F2作一条与x轴相交的直线l，分别与“月蚀圆”依次交于B、C、D、E四点，
（1）当直线l⊥x轴时，求
| |CD| |
| |BE| |
（2）当直线l不垂直x轴时，若G为CD中点、H为BE中点，问
| |CD|•|HF2| |
| |BE|•|GF2| |
考点：圆锥曲线的综合,直线与圆锥曲线的综合问题
专题：综合题
分析：（Ⅰ）因为在椭圆中2a=|AF1|+|AF2|=7+5=12，所以可求曲线C1方程．利用抛物线定义，可求曲线C2方程．
（Ⅱ）（1）当直线l⊥x轴时，直线l的方程为x=2，从而|CD|=8，|BE|=
，可得
的值；
（2）先设出B、C、D、E四点坐标，过F2作的与x轴不垂直的直线方程，分别与椭圆方程，抛物线方程联立，利用根与系数关系，求
的值，看结果是否为定值．
（Ⅱ）（1）当直线l⊥x轴时，直线l的方程为x=2，从而|CD|=8，|BE|=
| 32 |
| 3 |
| |CD| |
| |BE| |
（2）先设出B、C、D、E四点坐标，过F2作的与x轴不垂直的直线方程，分别与椭圆方程，抛物线方程联立，利用根与系数关系，求
| |CD|•|HF2| |
| |BE|•|GF2| |
解答：
解：（Ⅰ）设椭圆方程为
+
=1，
则2a=|AF1|+|AF2|=7+5=12，得a=6，…（2分）
设A（x，y），F1（-c，0），F2（c，0），
则（x+c）2+y2=72，（x-c）2+y2=52，
两式相减得xc=6，由抛物线定义可知|AF2|=x+c=5，
则c=2，x=3或x=2，c=3，
又∠AF2F1为钝角，则x=2，c=3舍去．…（4分）
所以椭圆方程为
+
=1，抛物线方程为y2=8x．…（6分）
（Ⅱ）（1）当直线l⊥x轴时，直线l的方程为x=2，从而|CD|=8，|BE|=
，
所以
=
；…（9分）
（2）当直线l不垂直x轴时，设B（x1，y1），E（x2，y2），C（x3，y3），D（x4，y4），
直线y=k（x-2），代入
+
=1得：8(
+2)2+9y2-288=0，即（8+9k2）y2+32ky-256k2=0，
则y1+y2=-
，y1y2=-
，
同理，将y=k（x-2）代入y2=8x得：ky2-8y-16k=0，
则y3+y4=
，y3y4=-16，
所以
=
=
=
为定值．…（14分）
| x2 |
| a2 |
| y2 |
| b2 |
则2a=|AF1|+|AF2|=7+5=12，得a=6，…（2分）
设A（x，y），F1（-c，0），F2（c，0），
则（x+c）2+y2=72，（x-c）2+y2=52，
两式相减得xc=6，由抛物线定义可知|AF2|=x+c=5，
则c=2，x=3或x=2，c=3，
又∠AF2F1为钝角，则x=2，c=3舍去．…（4分）
所以椭圆方程为
| x2 |
| 36 |
| y2 |
| 32 |
（Ⅱ）（1）当直线l⊥x轴时，直线l的方程为x=2，从而|CD|=8，|BE|=
| 32 |
| 3 |
所以
| |CD| |
| |BE| |
| 3 |
| 4 |
（2）当直线l不垂直x轴时，设B（x1，y1），E（x2，y2），C（x3，y3），D（x4，y4），
直线y=k（x-2），代入
| x2 |
| 36 |
| y2 |
| 32 |
| y |
| k |
则y1+y2=-
| 32k |
| 8+9k2 |
| 256k2 |
| 8+9k2 |
同理，将y=k（x-2）代入y2=8x得：ky2-8y-16k=0，
则y3+y4=
| 8 |
| k |
所以
| |CD|•|HF2| |
| |BE|•|GF2| |
|y3-y4|•
| ||
|y1-y2|•
|
|
| 1 |
| 3 |
点评：本题考查了椭圆，抛物线与直线的位置关系，掌握设而不求思想的应用是关键．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
已知平行四边形ABCD中，|