题目内容
求函数f（x）=x3-3x2在区间[-1，5]上的最值．
考点：利用导数求闭区间上函数的最值
专题：概率与统计
分析：由f（x）=x3-3x2，得f′（x）=3x2-6x，由f′（x）=3x2-6x=0，得x=0或x=2，由此能求出函数f（x）=x3-3x2在区间[-1，5]上的最值．
解答：
解：∵f（x）=x3-3x2，
∴f′（x）=3x2-6x，
由f′（x）=3x2-6x=0，得x=0或x=2，
列表，得：
∴函数f（x）=x3-3x2在区间[-1，5]上的最大值为f（5）=50，
最小值为f（-1）=f（2）=-4．
∴f′（x）=3x2-6x，
由f′（x）=3x2-6x=0，得x=0或x=2，
列表，得：
| x | -1 | （-1，0） | 0 | （0，2） | 2 | （2，5） | 5 |
| f′（x） | + | 0 | - | 0 | + | ||
| f（x） | -4 | ↑ | 0 | ↓ | -4 | ↑ | 50 |
最小值为f（-1）=f（2）=-4．
点评：本题考查函数在闭区间上的最大值和最小值的求法，考查实数的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
直线
x+y-2
=0的倾斜角为（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
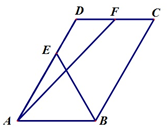已知平行四边形ABCD中，|