题目内容
设函数f(x)定义域为R,对于任意的x,y∈R,恒有f(x+y)=f(x)+f(y).
(Ⅰ)求f(0)的值;
(Ⅱ)判断函数的奇偶性.
(Ⅰ)求f(0)的值;
(Ⅱ)判断函数的奇偶性.
考点:函数奇偶性的性质,抽象函数及其应用
专题:函数的性质及应用
分析:(Ⅰ)令x=y=0,代入已知条件,即可求得结果;
(Ⅱ)令y=-x,代入已知条件由函数奇偶性的定义,即可判定函数的奇偶性.
(Ⅱ)令y=-x,代入已知条件由函数奇偶性的定义,即可判定函数的奇偶性.
解答:
解:(Ⅰ)∵f(x+y)=f(x)+f(y)对于任意x,y∈R都成立.
令x=y=0,则f(0)=f(0)+f(0)
解得f(0)=0;
(Ⅱ)函数f(x)是R上的奇函数.
证明:令y=-x,则f(0)=f(x)+f(-x)=0,
∴f(-x)=-f(x),
∴函数f(x)是R上的奇函数.
令x=y=0,则f(0)=f(0)+f(0)
解得f(0)=0;
(Ⅱ)函数f(x)是R上的奇函数.
证明:令y=-x,则f(0)=f(x)+f(-x)=0,
∴f(-x)=-f(x),
∴函数f(x)是R上的奇函数.
点评:本题考查抽象函数的有关问题,其中赋值法是常用的方法,考查函数的奇偶性的定义,属基础题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
已知tanαsinα<0且sinαcosα>0,则α所在象限为( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
如图,小圆圈表示网络的结点,结点之间的箭头表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点G传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )


| A、31 | B、6 | C、10 | D、14 |
直线
x+y-2
=0的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
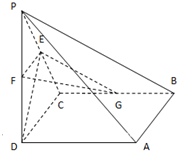 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E、F分别为PC、PD的中点.