题目内容
已知i是虚数单位,若
=1-i,则z的共轭复数为( )
| 3+i |
| z |
| A、1-2i | ||||
| B、2-4i | ||||
C、
| ||||
| D、1+2i |
考点:复数的基本概念
专题:数系的扩充和复数
分析:利用复数的运算法则及其共轭复数的意义即可得出.
解答:
解:∵
=1-i,
∴z=
=
=
=1+2i.
∴
=1-2i.
故选:A.
| 3+i |
| z |
∴z=
| 3+i |
| 1-i |
| (3+i)(1+i) |
| (1-i)(1+i) |
| 2+4i |
| 2 |
∴
. |
| z |
故选:A.
点评:本题考查了复数的运算法则及其共轭复数的意义,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
如图,在半径为R的圆C中,已知弦AB的长为5,则
•
=( )
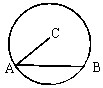
| AB |
| AC |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线的离心率为3,且它有一个焦点与抛物线y2=12x的焦点相同,那么双曲线的渐近线方程为( )
| A、x±2y=0 | ||
| B、2x±y=0 | ||
C、2
| ||
D、x±2
|
