题目内容
5.已知等差数列{an}的前n项和为Sn,a1=74,ak=2,S2k-1=194,则ak-40等于( )| A. | 66 | B. | 64 | C. | 62 | D. | 68 |
分析 设等差数列{an}的公差为d,由a1=74,ak=2,S2k-1=194,可得74+(k-1)d=2,S2k-1=194=$\frac{(2k-1)({a}_{1}+{a}_{2k-1})}{2}$=(2k-1)ak,解出即可得出.
解答 解:设等差数列{an}的公差为d,∵a1=74,ak=2,S2k-1=194,
∴74+(k-1)d=2,S2k-1=194=$\frac{(2k-1)({a}_{1}+{a}_{2k-1})}{2}$=(2k-1)ak,
解得k=49,d=-$\frac{3}{2}$.
则ak-40=a9=74-$\frac{3}{2}×8$=62.
故选:C.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
16.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x≤2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-1最大值为5.
20.若z=(m2-m-2)+(m2-2m-3)i为纯虚数,则m=( )
| A. | -1 | B. | 2 | C. | 3 | D. | -1或2 |
10.已知$\underset{lim}{△x→0}$$\frac{f{(x}_{0}+△x)-f{(x}_{0}-△x)}{△x}$=( )
| A. | $\frac{1}{2}$f′(x0) | B. | f′(x0) | C. | 2f′(x0) | D. | -f′(x0) |
14.设曲线y=ax-ln(2x+1)在点(0,0)处的切线方程为y=2x,则a=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.设α∈(0,π),sin α+cos α=$\frac{1}{3}$,则cos 2α的值是( )
| A. | $\frac{\sqrt{17}}{9}$ | B. | $\frac{-2\sqrt{2}}{3}$ | C. | -$\frac{\sqrt{17}}{9}$ | D. | $\frac{\sqrt{17}}{9}$或-$\frac{\sqrt{17}}{9}$ |
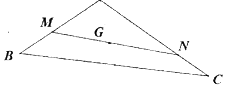 如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.
如图,已知点G是△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且$\overrightarrow{AM}$=$\frac{a}{3}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{b}{6}$$\overrightarrow{AC}$,则$\frac{2}{a-1}$+$\frac{1}{b-2}$的最小值为3.