题目内容
15.设α∈(0,π),sin α+cos α=$\frac{1}{3}$,则cos 2α的值是( )| A. | $\frac{\sqrt{17}}{9}$ | B. | $\frac{-2\sqrt{2}}{3}$ | C. | -$\frac{\sqrt{17}}{9}$ | D. | $\frac{\sqrt{17}}{9}$或-$\frac{\sqrt{17}}{9}$ |
分析 把已知等式两边平方,可得2sinαcosα<0,得到α∈($\frac{π}{2},π$),则sinα>0,cosα<0,进一步求得sinα-cosα,与原等式联立求出sinα,代入二倍角余弦求解.
解答 解:由sin α+cos α=$\frac{1}{3}$,两边平方得$si{n}^{2}α+co{s}^{2}α+2sinαcosα=\frac{1}{9}$,
∴$2sinαcosα=-\frac{8}{9}$,
又α∈(0,π),∴α∈($\frac{π}{2},π$),
则sinα>0,cosα<0,
∴sinα-cosα=$\sqrt{(sinα-cosα)^{2}}=\sqrt{1-2sinαcosα}$=$\sqrt{1+\frac{8}{9}}=\frac{\sqrt{17}}{3}$.
联立$\left\{\begin{array}{l}{sinα+cosα=\frac{1}{3}}\\{sinα-cosα=\frac{\sqrt{17}}{3}}\end{array}\right.$,得sinα=$\frac{\sqrt{17}+1}{6}$.
∴cos2α=1-2sin2α=1-2×$(\frac{\sqrt{17}+1}{6})^{2}$=$-\frac{\sqrt{17}}{9}$.
故选:C.
点评 本题考查二倍角的余弦,关键是由已知可得α∈($\frac{π}{2},π$),是中档题.

练习册系列答案
相关题目
5.已知等差数列{an}的前n项和为Sn,a1=74,ak=2,S2k-1=194,则ak-40等于( )
| A. | 66 | B. | 64 | C. | 62 | D. | 68 |
6.在△ABC中,$a=2\sqrt{2},b=3,A=45°$,则此三角形解的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
3.已知点A(-1,0),B(1,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-y2=1 | D. | x2-$\frac{{y}^{2}}{2}$=1 |
20.用反证法证明命题:“若a,b∈Z,ab能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A. | a,b都能被5整除 | B. | a,b都不能被5整除 | ||
| C. | a,b有一个能被5整除 | D. | a,b有一个不能被5整除 |
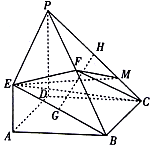 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.