题目内容
16.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x≤2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-1最大值为5.分析 先根据约束条件画出可行域,再利用几何意义求最值,z=2x-2y-1表示直线在y轴上的截距的一半减去$\frac{1}{2}$,只需求出可行域的最优解代入求解即可.
解答  解:先根据实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x≤2}\\{x+y-1≥0}\end{array}\right.$,画出可行域,
解:先根据实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x≤2}\\{x+y-1≥0}\end{array}\right.$,画出可行域,
当直线z=2x-2y-1过点A时,截距的一半减去$\frac{1}{2}$最小,此时
z最大,由$\left\{\begin{array}{l}{x=2}\\{x+y-1=0}\end{array}\right.$,可得A(2,-1)
z的最大值为:2×2-2×(-1)-1=5.
故答案为:5.
点评 本小题主要考查线性规划问题,以及利用几何意义求最值,属于中档题.

练习册系列答案
相关题目
7.将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得g(x)的图象,若对满足f(x1)•g(x2)=-1的任意x1,x2,都有|x1-x2|min=$\frac{π}{4}$,则φ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{3}$ |
4. 为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
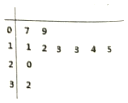
从本市随机抽取了10户家庭,统计了同一个月的用水量,得到如图所示的茎叶图.
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
 为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:| 阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
| 月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
11.设集合A={x|x2-x-2<0},集合B={x|-1<x≤1},则A∩B=( )
| A. | [-1,1] | B. | (-1,1] | C. | (-1,2) | D. | [1,2) |
8.设随机变量ξ~N(2,1),若P(ξ>3)=m,则p(1<ξ<3)等于( )
| A. | $\frac{1}{2}$-2m | B. | 1-m | C. | 1-2m | D. | $\frac{1}{2}$-m |
5.已知等差数列{an}的前n项和为Sn,a1=74,ak=2,S2k-1=194,则ak-40等于( )
| A. | 66 | B. | 64 | C. | 62 | D. | 68 |
6.在△ABC中,$a=2\sqrt{2},b=3,A=45°$,则此三角形解的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |