题目内容
已知点P是抛物线y2=4x上的动点，F是该抛物线的焦点，点A的坐标是（4，a），则当|a|＜4时，|PA|+|PF|的最小值是 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由P向准线x=-1作垂线，垂足为M，由抛物线的定义，PF=PM，当且仅当A，P，M三点共线时，|PA|+|PF|取得最小值．
解答：
解：由P向准线x=-1 作垂线，垂足为M，由抛物线的定义，PF=PM，再由定点A向准线作垂线，垂足为N，
那么点P在该抛物线上移动时，有PA+PF=PA+PM≥AN，当且仅当A，P，N三点共线时，
取得最小值AN=4-（-1）=5，
此时|PA|+|PF|取得最小值5
故答案为：5
那么点P在该抛物线上移动时，有PA+PF=PA+PM≥AN，当且仅当A，P，N三点共线时，
取得最小值AN=4-（-1）=5，
此时|PA|+|PF|取得最小值5
故答案为：5
点评：本题主要考查抛物线的定义、标准方程，以及简单性质的应用，属于中档题．
练习册系列答案
相关题目
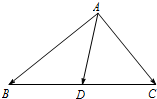如图，点D是线段BC的中点，BC=6，且|| AB |
| AC |
| AB |
| AC |
| AD |
| A、6 | ||
B、2
| ||
| C、3 | ||
D、
|
函数f（x）=x+
+3在（-∞，0）上（ ）
| 4 |
| x |
| A、有最大值-1，无最小值 |
| B、无最大值，有最小值-1 |
| C、有最大值7，有最小值-1 |
| D、无最大值，有最小值7 |
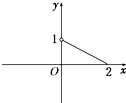已知定义在[-2，2]上的奇函数f（x）在（0，2]上的图象如图所示，