Question

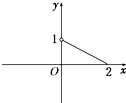已知定义在[-2，2]上的奇函数f（x）在（0，2]上的图象如图所示，
（1）求f（x）的解析式；
（2）并求不等式f（x）＞x．

Answer 1

考点：函数奇偶性的性质

专题：计算题,函数的性质及应用,不等式的解法及应用

分析：（1）可设x∈（0，2]，f（x）=kx+b（k≠0），代入数据，列出方程，解得即可得到，令-2≤x＜0，则0＜-x≤2，再由已得的表达式以及奇函数的定义，即可得到；
（2）不等式f（x）＞x即为

-2≤x＜0 - 1 2 x-1＞x

或

0＜x≤2 - 1 2 x+1＞x

或

x=0 0＞x

，分别解出它们，最后求并集即可．

解答： 解：（1）由图可设x∈（0，2]，f（x）=kx+b（k≠0）
根据图象有

f(0)=1 f(2)=0

，解得

k=- 1 2 b=1

，所以x∈(0，2]，f(x)=-

1

2

x+1；
令-2≤x＜0，则0＜-x≤2，则有f（-x）=

1

2

x+1，
又f（x）为奇函数，则f（-x）=-f（x），
即f（x）=-

1

2

x-1（x∈[-2，0）），又f（0）=0，
则f（x）=

- 1 2 x-1，-2≤x＜0 0，x=0 - 1 2 x+1，0＜x≤2

；
（2）不等式f（x）＞x即为

-2≤x＜0 - 1 2 x-1＞x

或

0＜x≤2 - 1 2 x+1＞x

或

x=0 0＞x

，
即有-2≤x＜-

2

3

或0＜x＜

2

3

或x∈∅，
则原不等式的解集为：[-2，-

2

3

）∪（0，

2

3

）．

点评：本题考查函数的解析式的求法：待定系数法，考查分段函数的运用：解不等式，注意各段的情况，考查运算能力，属于中档题．