题目内容
设变量x,y满足约束条件
,则目标函数z=-x+y的最大值是 .
|
考点:简单线性规划
专题:数形结合,不等式的解法及应用
分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,求得最优解,把最优解的坐标代入目标函数得答案.
解答:
解:由约束条件
作出可行域如图,

化目标函数z=-x+y为y=x+z,
由图可知,当直线y=x+z过B(0,2)时,z有最大值,为2.
故答案为:2.
|

化目标函数z=-x+y为y=x+z,
由图可知,当直线y=x+z过B(0,2)时,z有最大值,为2.
故答案为:2.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知a,b∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lg(a-b)>0 | ||||
D、(
|
若x、y满足约束条件
目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
|
| A、(-4,2) |
| B、(-1,2) |
| C、(-4,0) |
| D、(-2,4) |
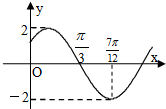 如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x-
| ||||
D、y=2sin(2x+
|
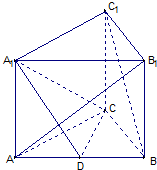 如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.
如图:直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=2,D为AB中点.