题目内容

函数f（x）=x+
4
x
+3在（-∞，0）上（　　）
A、有最大值-1，无最小值
B、无最大值，有最小值-1
C、有最大值7，有最小值-1
D、无最大值，有最小值7
考点：基本不等式
专题：不等式的解法及应用
分析：由x∈（-∞，0），可得-x∈（0，+∞）．变形f（x）=x+
4
x
+3=-(-x+
4
-x
)+3，利用基本不等式的性质即可得出．
解答： 解：∵x∈（-∞，0），∴-x∈（0，+∞）．
∴f（x）=x+
4
x
+3=-(-x+
4
-x
)+3≤-2
(-x)•
4
-x
+3=-1，当且仅当x=-2时取等号．
∴函数f（x）=x+
4
x
+3在（-∞，0）上有最大值-1，无最小值．
故选：A．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
已知a，b∈R，且a＞b，则（　　）
A、a2＞b2
B、
a
b
＞1
C、lg（a-b）＞0
D、(
1
2
)a＜(
1
2
)b
已知点P是抛物线y2=4x上的动点，F是该抛物线的焦点，点A的坐标是（4，a），则当|a|＜4时，|PA|+|PF|的最小值是
 
．
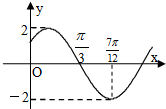如图是函数y=Asin（ωx+φ）（A＞0，ω＞0）的部分图象，则下列可以作为其解析式的是（　　）
A、y=2sin（2x-
π
3
）
B、y=2sin（
1
2
x+
π
3
）
C、y=2sin（2x-
2π
3
）
D、y=2sin（2x+
π
3
）
圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0的距离的最小值是
 
，最大值是
 
．
已知命题p：?x∈R，2x＞0；命题q：在曲线y=cosx上存在斜率为
2
的切线，则下列判断正确的是（　　）
A、p是假命题
B、q是真命题
C、p∧（￢q）是真命题
D、（￢p）∧q是真命题
在△ABC中，a，b，c分别为角A、B、C的对边，若边a，b，c成等差数列，则∠B的范围是（　　）
A、0＜B≤
π
6
B、0＜B≤
π
3
C、0＜B≤
π
2
D、
π
2
＜B＜π
求函数f（x）=
1+sinx
+
1-sinx
+
2+sinx
+
2-sinx
+
3+sinx
+
3-sinx
的最大值．
直线3x+y-3=0与直线6x+my+1=0垂直，则m的值为（　　）
A、2B、-2C、18D、-18

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网