题目内容

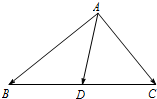如图，点D是线段BC的中点，BC=6，且|
AB
+
AC
|=|
AB
-
AC
|，则|
AD
|=（　　）
A、6
B、2
3
C、3
D、
3
2
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由于向量的平方即为模的平方，将等式两边平方，化简可得
AB
•
AC
=0，即
AB
⊥
AC
，则△ABC为直角三角形，再由斜边上的中线等于斜边的一半，即可得到答案．
解答： 解：由于|
AB
+
AC
|=|
AB
-
AC
|，
则两边平方得，|
AB
+
AC
|2=|
AB
-
AC
|2，
即有
AB
2+
AC
2+2
AB
•
AC
=
AB
2+
AC
2-2
AB
•
AC
，
即有
AB
•
AC
=0，
即
AB
⊥
AC
，
则△ABC为直角三角形，BC为斜边，AD为斜边上的中线，
则|
AD
|=
1
2
|
BC
|=3．
故选C．
点评：本题考查平面向量的运用，考查向量数量积的性质：向量的平方即为模的平方，考查直角三角形的性质，属于中档题．
练习册系列答案
相关题目
已知数列{an}是公差d=2的等差数列，且a2，a3，a4+1成等比
（1）求数列{an}的通项公式；
（2）令bn=an+2n，求数列{bn}前n项和Sn．
已知非零实数θ满足等式：16θ+
1
θ
=16sinπθcosπθ，则θ=
 
．
已知a，b∈R，且a＞b，则（　　）
A、a2＞b2
B、
a
b
＞1
C、lg（a-b）＞0
D、(
1
2
)a＜(
1
2
)b
先后抛掷两颗均匀的骰子，问：
（1）至少有一颗是5点的概率是多少？
（2）当第一颗骰子的点数为3或6时，求两颗骰子的点数之和大于8的概率．
已知平面向量
a
=（2，-1），
b
=（x，1），若
a
⊥
b
，则x=
 
．
平面直角坐标系中，方程|x-1|+|y-1|=1的曲线围成的封闭图形绕y轴旋转一周所形成的几何体的体积为
 
．
已知点P是抛物线y2=4x上的动点，F是该抛物线的焦点，点A的坐标是（4，a），则当|a|＜4时，|PA|+|PF|的最小值是
 
．
在△ABC中，a，b，c分别为角A、B、C的对边，若边a，b，c成等差数列，则∠B的范围是（　　）
A、0＜B≤
π
6
B、0＜B≤
π
3
C、0＜B≤
π
2
D、
π
2
＜B＜π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网