题目内容
已知等差数列{an}的公差为d>0,首项a1=3,且a1+2,a2+5,a3+13分别为等比数列{bn}中的b3,b4,b5,求数列{bn}的公比q和数列{an}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:直接由a1+2,a2+5,a3+13成等比数列求出等差数列的公差,进一步得到等比数列的公比,代入等比数列的前n项和公式得答案.
解答:
解:∵a1+2,a2+5,a3+13分别为等比数列{bn}中的b3,b4,b5,
∴(a2+5)2=(a1+2)(a3+13),
即(8+d)2=5(16+2d),得d=2.
∴q=
=
=2.
∴数列{an}的前n项和Sn=3n+
×2=n2+2n.
∴(a2+5)2=(a1+2)(a3+13),
即(8+d)2=5(16+2d),得d=2.
∴q=
| a2+5 |
| a1+2 |
| 10 |
| 5 |
∴数列{an}的前n项和Sn=3n+
| n(n-1) |
| 2 |
点评:本题考查了等差数列的通项公式,考查了等比数列的性质,考查了等比数列的前n项和,是基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
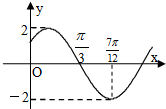 如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象,则下列可以作为其解析式的是( )A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x-
| ||||
D、y=2sin(2x+
|
在△ABC中,a,b,c分别为角A、B、C的对边,若边a,b,c成等差数列,则∠B的范围是( )
A、0<B≤
| ||
B、0<B≤
| ||
C、0<B≤
| ||
D、
|