题目内容
函数f(x)=lnx-
.
(1)当a=-2时,求f(x)的最小值;
(2)若f(x)在[1,e]上的最小值为
,求a的值.
| a |
| x |
(1)当a=-2时,求f(x)的最小值;
(2)若f(x)在[1,e]上的最小值为
| 3 |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)把a=-2代入函数解析式,求导后由导函数在定义域内不同区间内的符号得到原函数的单调期间,找到极小值点,求出极小值,也就是最小值;
(2)求出原函数的导函数f′(x)=
+
=
,然后分a≥-1、a≤-e、-e<a<-1借助于导数分析原函数在[1,e]上的单调性,由单调性求得最小值,由最小值为
求得a的值.
(2)求出原函数的导函数f′(x)=
| 1 |
| x |
| a |
| x2 |
| x+a |
| x2 |
| 3 |
| 2 |
解答:
解:(1)当a=-2时,f(x)=ln x+
,f′(x)=
,
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
∴f(x)min=f(2)=ln 2+1;
(2)f′(x)=
+
=
,
①当a≥-1时,对任意x∈[1,e],
f′(x)≥0,此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=
,
∴a=-
(舍).
②当a≤-e时,对任意x∈[1,e],
f′(x)≤0,此时f(x)在[1,e]上为减函数.
∴f(x)min=f(e)=1-
=
.
∴a=-
(舍).
③当-e<a<-1时,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
f(x)在(1,-a)上递减.同理,f(x)在(-a,e)上递增.
∴f(x)min=f(-a)=ln(-a)+1=
,
∴a=-
.综上,a=-
.
| 2 |
| x |
| x-2 |
| x2 |
当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
∴f(x)在(0,2)上为减函数,在(2,+∞)上为增函数.
∴f(x)min=f(2)=ln 2+1;
(2)f′(x)=
| 1 |
| x |
| a |
| x2 |
| x+a |
| x2 |
①当a≥-1时,对任意x∈[1,e],
f′(x)≥0,此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=
| 3 |
| 2 |
∴a=-
| 3 |
| 2 |
②当a≤-e时,对任意x∈[1,e],
f′(x)≤0,此时f(x)在[1,e]上为减函数.
∴f(x)min=f(e)=1-
| a |
| e |
| 3 |
| 2 |
∴a=-
| e |
| 2 |
③当-e<a<-1时,令f′(x)=0,得x=-a,当1<x<-a时,f′(x)<0,
f(x)在(1,-a)上递减.同理,f(x)在(-a,e)上递增.
∴f(x)min=f(-a)=ln(-a)+1=
| 3 |
| 2 |
∴a=-
| e |
| e |
点评:本题考查了利用导数求闭区间上函数的最值,考查了分类讨论的数学思想方法,求函数在闭区间[a,b]上的最大值与最小值是通过比较函数在(a,b)内所有极值与端点函数f(a),f(b) 比较而得到的,是中档题.

练习册系列答案
相关题目
若x=-
是f(x)=cosx+asinx的对称轴,则f(x)=cosx+asinx的初相是( )
| π |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
设a∈R,若函数y=ex+3ax(x∈R)有小于零的极值点,则( )
| A、-3<a<0 | ||
B、-
| ||
| C、a<-3 | ||
D、a<-
|
若f′(x0)=-3,则
=( )
| lim |
| h→∞ |
| f(x0-3h)-f(x0) |
| h |
| A、-3 | B、-6 | C、9 | D、12 |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.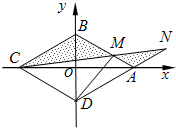 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).