题目内容
若x=-
是f(x)=cosx+asinx的对称轴,则f(x)=cosx+asinx的初相是( )
| π |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数
专题:三角函数的求值,三角函数的图像与性质
分析:首先根据函数的对称轴建立关于a的方程求出a值,进一步对f(x)=cosx+asinx的关系进行恒等变换,整理成f(x)=2sin(x+
)的形式,最后求出结果.
| 5π |
| 6 |
解答:
解:已知x=-
是f(x)=cosx+asinx的对称轴,
所以cos(-
)+asin(-
)=±
,
解得:a=-
,
则:f(x)=cosx-
sinx=2sin(x+
),
故选:C.
| π |
| 3 |
所以cos(-
| π |
| 3 |
| π |
| 3 |
| 1+a2 |
解得:a=-
| 3 |
则:f(x)=cosx-
| 3 |
| 5π |
| 6 |
故选:C.
点评:本题考查的知识点:正弦型函数的最值与对称轴的关系,三角恒等变换,函数的初相.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
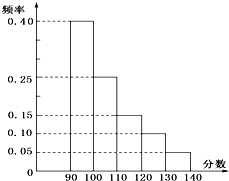 某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为( )
某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为( )| A、740 | B、180 |
| C、720 | D、540 |
已知-1,x,-4成等比数列,则x的值为( )
| A、2 | ||||
B、-
| ||||
| C、2 或-2 | ||||
D、-
|