题目内容
函数y=
的单调递增区间为 .
| x-1 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:先求出函数的定义域,再根据复合函数“同增异减”的性质,从而求出函数的单调区间.
解答:
解:∵x-1≥0,
∴函数的定义域是:[1,+∞),
又y=
,y=x-1同为增函数,
∴y=
在定义域单调递增,
故答案为:[1,+∞).
∴函数的定义域是:[1,+∞),
又y=
| x |
∴y=
| x-1 |
故答案为:[1,+∞).
点评:本题考查了复合函数的单调性,考查了二次函数的定义域,是一道基础题.

练习册系列答案
相关题目
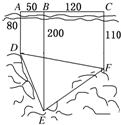 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,则∠DEF的余弦值为( )
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,则∠DEF的余弦值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=(
) x2+2(a-1)x+2在区间(-∞,4]上单调递增,那么实数a的取值范围是( )
| 1 |
| 2 |
| A、a≤-3 | B、a≥-3 |
| C、a≤5 | D、a≥5 |
已知a=3-
,b=log2
,c=log
,则( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |
二项式(x2-
)9的展开式中的常数项为( )
| 1 |
| x |
| A、36 | B、-36 |
| C、84 | D、-84 |
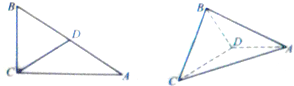 在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.
在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.