题目内容
已知a=3-
，b=log2
，c=log
，则（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、c＞b＞a |
考点：对数值大小的比较
专题：函数的性质及应用
分析：判断a、b、c与1，0的大小，即可得到结果．
解答：
解：a=3-
∈（0，1），b=log2
＜0，c=log
＞1．
∴c＞a＞b．
故选：C．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴c＞a＞b．
故选：C．
点评：本题考查函数值的大小比较，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
等比数列{an}中，已知a3•a10=8a52，a2=2，则a1=（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
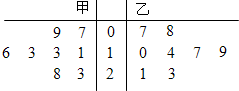某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图：若以甲、乙两名队员得分的频率作为概率，假设甲、乙两名队员在同一场比赛中的得分互不影响．
已知函数f（x）=ax+b（a＞0，a≠1）的图象如图所示，则a-b的值为